十二相同步整流发电机的数学模型

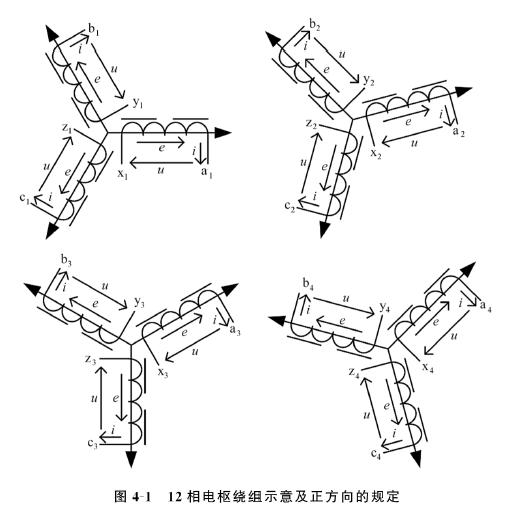
假设条件与正方向

与常规同步发电机相比，多相整流发电机除了定子结构有差异，其转子也会有一定的区别。为了改善其运行稳定性,在常规同步发电机转子设置的励磁绕组($fd$)、d轴阻尼绕组($kd$)和q轴阳阻尼绕组($kq$)三套绕组基础上，还会布置q轴稳定绕组($fq$)。为了简化分析过程，并确保一定的分析精度，对十二相发电机的物理状态作如下基本假设:

• 忽略铁心材料的饱和、磁滞及涡流影响，不计导线的集肤效应；
• 忽略空间谐波磁场的影响，气隙磁场按正弦分布；
• 忽略定、转子齿槽影响，认为定子和转子表面光滑；
• 将转子上的阻尼回路看作两组等效的阻尼绕组，即$D$轴阻尼绕组和$Q$轴阻尼绕组。

正方向规定如下：

• 定子绕组电路采用发电机惯例，转子绕组电路采用电动机惯例；
• 正方向的定子电流产生负的磁链，正方向的转子电流产生正的磁链；
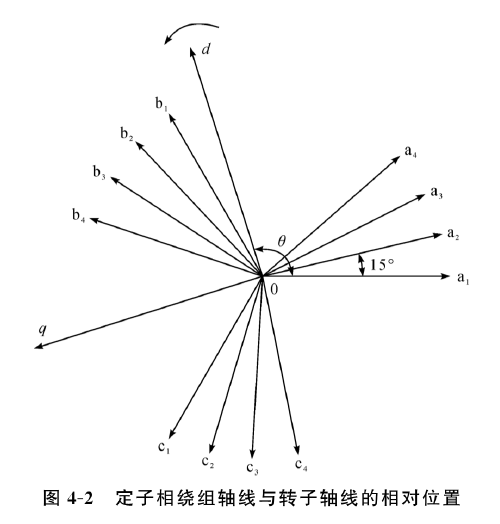
• 转子旋转正方向为逆时针方向，$q$轴正方向领先$d$轴正方向90°电角度。

abc坐标系下的基本方程

磁链参数矩阵为：

$$\Psi_{abc}= \begin{bmatrix} \Psi_{a1} & \Psi_{b1} & \Psi_{c1} & \Psi_{a2} & \Psi_{b2} & \Psi_{c2} & \Psi_{a3} & \Psi_{b3} & \Psi_{c3} & \Psi_{a4} & \Psi_{b4} & \Psi_{c4} & \Psi_{fd} & \Psi_{kd} & \Psi_{fq} & \Psi_{kq} \end{bmatrix}^T$$

式中前12项下标为12个相位的标号，后四项中

• $\Psi_{fd}$：励磁绕组磁链
• $\Psi_{kd}$：直轴阻尼绕组磁链
• $\Psi_{fq}$：交轴稳定绕组磁链
• $\Psi_{kq}$：交轴阻尼绕组磁链

电压参数矩阵为

$$u_{abc}= \begin{bmatrix} u_{a1} & u_{b1} & u_{c1} & u_{a2} & u_{b2} & u_{c2} & u_{a3} & u_{b3} & u_{c3} & u_{a4} & u_{b4} & u_{c4} & u_{fd} & u_{kd} & u_{fq} & u_{kq} \end{bmatrix}^T$$

电流参数矩阵为

$$i_{abc}= \begin{bmatrix} i_{a1} & i_{b1} & i_{c1} & i_{a2} & i_{b2} & i_{c2} & i_{a3} & i_{b3} & i_{c3} & i_{a4} & i_{b4} & i_{c4} & i_{fd} & i_{kd} & i_{fq} & i_{kq} \end{bmatrix}^T$$

因直轴阻尼绕组、交轴阻尼绕组和交轴稳定绕组均短接，有$u_{kd}=u_{kq}=u_{fq}=0$。

相应的磁链方程和电压方程为

$$\Psi_{abc}=L_{abci}i_{abc} \\ u_{abc}=p\Psi_{abc}-R_{abc}i_{abc}$$

式中

$$L_{abc}= \begin{bmatrix} L_{11} & L_{12} & L_{13} & L_{14} & L_{1r} \\ L_{21} & L_{22} & L_{23} & L_{24} & L_{2r} \\ L_{31} & L_{32} & L_{33} & L_{34} & L_{3r} \\ L_{41} & L_{42} & L_{43} & L_{44} & L_{4r} \\ -L_{1r}^T & -L_{2r}^T & -L_{3r}^T & -L_{4r}^T & L_{rr} \\ \end{bmatrix}$$

式中$L_{ij},i=1,2,3,4;i=1,2,3,4$为分块矩阵，具体为

$$L_{ij}= \begin{bmatrix} -L_{aiaj} & -L_{aibj} & -L_{aicj} \\ -L_{biaj} & -L_{bibj} & -L_{bicj} \\ -L_{ciaj} & -L_{cibj} & -L_{cicj} \\ \end{bmatrix}$$

矩阵中$-L_{aiaj}$表示$ai$相电枢绕组与$aj$相电枢绕组之间的互感/自感。因正方向中规定正方向的定子电流产生负的磁链，所以所有电感均带负号。

同理，式中$L_{ir},i=1,2,3,4$也为分块矩阵，具体为

$$L_{ir}= \begin{bmatrix} L_{aifd} & L_{aikd} & L_{aifq} & L_{aikq} \\ L_{bifd} & L_{bikd} & L_{bifq} & L_{bikq} \\ L_{cifd} & L_{cikd} & L_{cifq} & L_{cikq} \\ \end{bmatrix}$$

矩阵中$L_{aifd}$表示电枢$ai$相绕组与转子励磁绕组的互感，其余同理。因正方向中规定正方向的转子电流产生正的磁链，所以所有电感均为正。

同理，式中$L_{rr}$表示转子各绕组之间的自感/互感，具体为

$$L_{rr}= \begin{bmatrix} L_{fd} & L_{fdkd} & 0 & 0 \\ L_{fdkd} & L_{kd} & 0 & 0 \\ 0 & 0 & L_{fq} & L_{fqkq} \\ 0 & 0 & L_{fqkq} & L_{kq} \\ \end{bmatrix}$$

矩阵中$L_{fd}$为励磁绕组的自感，$L_{fdkd}$为励磁绕组与直轴阻尼绕组的互感，其余同理。因为励磁绕组与交轴阻尼绕组、励磁绕组与交轴稳定绕组、直轴阻尼绕组与交轴阻尼绕组、直轴阻尼绕组与交轴稳定绕组的电角度夹角均为90$\degree$，所以有$L_{fdkq}=L_{fdfq}=L_{kdkq}=L_{kdfq}=0$。

电感矩阵中各量的详细表达式略。

dq0坐标系下的基本方程

变换矩阵

应用推广的三相电机Park变换，取变换矩阵为

$$C^{abc}_{dq0}(\theta)= \begin{bmatrix} C_{11} & & & & \\ & C_{22} & & & \\ & & C_{33} & & \\ & & & C_{44} & \\ & & & & I \\ \end{bmatrix}$$

式中$I$为$4\times 4$的单位矩阵，其对应的变换对象为转子部分参数，显然该部分无需进行Park变换。

式中，

$$C_{ii}= \frac{2}{3} \begin{bmatrix} \cos[\theta-(i-1)15\degree] & \cos[\theta-120\degree-(i-1)15\degree] & \cos[\theta+120\degree-(i-1)15\degree] \\ -\sin[\theta-(i-1)15\degree] & -\sin[\theta-120\degree-(i-1)15\degree] & -\sin[\theta+120\degree-(i-1)15\degree] \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2}\\ \end{bmatrix}$$

电压方程

展开dq0坐标系下的有名值电压方程式得

$$\begin{bmatrix} u_{d1} \\ u_{q1} \\ u_{01} \\ u_{d2} \\ u_{q2} \\ u_{02} \\ u_{d3} \\ u_{q3} \\ u_{03} \\ u_{d4} \\ u_{q4} \\ u_{04} \\ u_{fd} \\ u_{kd} \\ u_{fq} \\ u_{kq} \\ \end{bmatrix} = p \begin{bmatrix} \Psi_{d1} \\ \Psi_{q1} \\ \Psi_{01} \\ \Psi_{d2} \\ \Psi_{q2} \\ \Psi_{02} \\ \Psi_{d3} \\ \Psi_{q3} \\ \Psi_{03} \\ \Psi_{d4} \\ \Psi_{q4} \\ \Psi_{04} \\ \Psi_{fd} \\ \Psi_{kd} \\ \Psi_{fq} \\ \Psi_{kq} \\ \end{bmatrix} + \begin{bmatrix} -\omega \Psi_{q1} \\ \omega \Psi_{d1} \\ 0 \\ -\omega \Psi_{q2} \\ \omega \Psi_{d2} \\ 0 \\ -\omega \Psi_{q3} \\ \omega \Psi_{d3} \\ 0 \\ -\omega \Psi_{q4} \\ \omega \Psi_{d4} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{bmatrix} + \begin{bmatrix} - r_s i_{d1} \\ -r_s i_{q1} \\ -r_s i_{01} \\ - r_s i_{d2} \\ -r_s i_{q2} \\ -r_s i_{02} \\ - r_s i_{d3} \\ -r_s i_{q3} \\ -r_s i_{03} \\ - r_s i_{d4} \\ -r_s i_{q4} \\ -r_s i_{04} \\ r_{fd} i_{fd}\\ r_{fq} i_{fq}\\ r_{kd} i_{kd}\\ r_{kq} i_{kq} \\ \end{bmatrix}$$

考虑基值选取中有$\omega_B$的存在，将电压方程定子侧的第一个矩阵（磁链阵）除以之，可得$x_{ad}$基值系统下的标幺值定子电压方程：

$$$$