十二相同步整流发电机模型推导

引言

十二相同步发电机在定转子分解方面的步骤和三相同步发电机基本一致。如果单独考虑与定子直轴和交轴绕组想独立的零轴绕组，则在考虑$d$、$q$、$f$、$D$、$Q$五个绕组的电磁过渡过程及转子机械过渡过程时，会面临高阶模型的求解难题。实际工程中通常对同步电机的数学模型作不同程度的简化。

参数定义

符号	含义	单位
$u_d$	定子d轴电压	V（伏）
$u_q$	定子q轴电压	V（伏）
$i_d$	定子d轴电流	A（安）
$i_q$	定子q轴电流	A（安）
$r_a$	定子各相绕组电阻	Ω（欧姆）
$X_d$	直轴同步电抗	Ω（欧姆）
$X_q$	交轴同步电抗	Ω（欧姆）
$X_d'$	直轴暂态电抗	Ω（欧姆）
$X_{ad}$	直轴电枢反应电抗	Ω（欧姆）
$X_{aq}$	交轴电枢反应电抗	Ω（欧姆）
$X_f$	励磁绕组自感电抗	Ω（欧姆）
$r_f$	励磁绕组电阻	Ω（欧姆）
$E_q$	交轴空载电动势（稳态）	V（伏）
$E_q'$	交轴暂态电动势（状态变量）	V（伏）
$E_f$	等效励磁电动势（励磁系统输入）	V（伏）
$T_{d0}'$	d轴开路暂态时间常数	s（秒）
$T_J$	转子转动惯量对应时间常数	s（秒）
$T_m$	原动机提供的机械转矩	Nm（牛·米）
$T_e$	发电机电磁转矩	Nm（牛·米）
$\omega$	电机相对同步角速度（机械量）	p.u.（标幺值）
$\delta$	电机转子与同步旋转坐标系的夹角	rad（弧度）
$\Phi_d$	d轴磁链	Wb（韦伯）
$\Phi_q$	q轴磁链	Wb（韦伯）
$\Phi_f$	励磁绕组磁链	Wb（韦伯）
$p$	微分算符（$p = \frac{d}{dt}$）	s⁻¹（每秒）

前置条件

假定：

• 忽略定子直轴、交轴绕组的暂态过程，即定子电压方程中取$p\Phi_d=p\Phi_q=0$
• 在定子电压方程中取$\omega \approx 1(p.u.)$。通常在速度变化不大的过渡过程中，该近似引起的误差较小
• 忽略$D$、$Q$和等效交轴稳定绕组，其作用可在转子运动方程补入阻尼项来近似

推导

引入实用变量

为了消去转子励磁绕组的变量$i_f$、$u_f$和$\Phi_f$，引入以下三个定子侧等效实用变量：

1. 定子励磁电动势$E_f$：

$$E_f = X_{ad}\frac{u_f}{r_f}$$

2. 交轴空载电动势$E_q$

$$E_q = X_{ad}i_f$$

3. 交轴瞬变电动势$E_q'$

$$E_q' = \frac{X_{ad}}{X_f}\Phi_f$$

也就是说$E_f$、$E_q$、$E_q'$分别对应$u_f$、$i_f$、$\Phi_f$。

稳态时，有$i_f = u_f / r_f$，所以(下标0表示稳态值):

$$E_{f0} = E_{q0}$$

由Park方程，稳态时

$$u_{q0} = E_{q0} - X_d i_{d0} - r_a i_{q0}$$

从而

$$E_{f0} = E_{q0} = u_{q0} + X_d i_{d0} + r_a i_{q0}$$

根据上式可由稳态定子电量计算$E_{f0}$ 和 $E_{q0}$。

根据$E_q' = \frac{X_{ad}}{X_f}\Phi_f$，电机交轴瞬变电动势$E_q'$和励磁绕组磁链成正比，由于暂态过程中磁链无法突变，假设扰动发生在$t=0$，则

$$E_q'|_{t=0} = E_q'|_{t=0'}$$

可根据稳态值来确定$E_q'$在扰动发生时的初值，而由Park方程可知

$$\Phi_{f0} = -X_{ad}i_{d0} + X_f i_{f0}$$

等式两侧同乘$X_{ad}/X_f$，可得

$$E_{q0}' = \frac{X_{ad}}{X_f}\Phi_{f0} = - \frac{X_{ad}^2}{X_f}i_{d0} + X_{ad}i_{f0}$$

根据$E_{f0} = E_{q0} = u_{q0} + X_d i_{d0} + r_a i_{q0}$，有

$$X_{ad}i_{f0} = E_{q0} = u_{q0} + X_di_{d0} + r_a i_{q0}$$

因为

$$X_d' = X_d - \frac{X_{ad}^2}{X_f}$$

代入$E_{q0}' = \frac{X_{ad}}{X_f}\Phi_{f0} = - \frac{X_{ad}^2}{X_f}i_{d0} + X_{ad}i_{f0}$，可得

$$E_{q0}' = u_{q0} + X_d'i_{d0}+r_ai_{q0}$$

该式可用于计算$E_q'$在扰动时的初值，$E_{q0}'$反映了瞬变初的交轴暂态电动势。

导出思路

思路如下：

1. 对于Park方程，在忽略$D$、$Q$绕组（将相应方程及变量删去）后，尚有以下变量：$u_{dqf}$、$i_{dqf}$、$\Phi_{dqf}$及$\omega$、$\delta$、$T_m$。假设$u_f$和$T_m$为已知量（分别为励磁系统及原动机输出量），则有10个未知量。对应有直轴、交轴和励磁3个绕组的电压方程、磁链方程和2个转子运动方程，共计8个方程。若和直轴、交轴网络方程联立，则变量数和方程数平衡，可以求解。
2. 由Park方程推导三阶实用模型时，应保留定子变量$u_{dq}$和$i_{dq}$，而转子变量$u_f$、$i_f$和$\Phi_f$分别用$E_f$、$E_q$和$E_q'$替代，然后再用3个磁链方程消去$\Phi_d$、$\Phi_q$及$i_f$（或$E_q$），从而在最终同步电机模型中保留$u_{dq}$、$i_{dq}$、$E_f$、$E_q'$及$\omega$、$\delta$、$T_m$等变量，其中$E_q'$、$\omega$、$\delta$为状态量，电机方程由3个电压方程和2个转子运动方程组成。当$E_f$和$T_m$已知时（对外表现为励磁系统和原动机系统输入），可联立求解方程。

变量转换及消去

先消去$\Phi_d$、$\Phi_q$及$i_f$（$E_q$）所用表达式，将其用保留变量的函数来表示。

已知直轴磁链方程为：

$$\Phi_d = -X_di_d + X_{ad}i_f$$

$$\Phi_f = -X_{ad}i_d + X_{f}i_f$$

将上式中的第二个式子等式两侧同乘$X_{ad}/X_f$，有

$$E_q' = -\frac{X_{ad}^2}{X_f}i_d + X_{ad}i_f$$

因为

$$X_d' = X_d - \frac{X_{ad}^2}{X_f}$$

则上上个式子可表示为

$$E_q' = \Phi_d + X_d'i_d$$

或

$$\Phi_d = E_q' - X_d'i_d$$

上式即可用来消去$\Phi_d$。

由$\Phi_d = -X_di_d + X_{ad}i_f$和$E_q = X_{ad}i_f$，可得

$$\Phi_d = E_q - X_di_d$$

将$\Phi_d = E_q' - X_d'i_d$代入上式，可得

$$E_q' - X_d'i_d = E_q - X_di_d$$

整理，上式即为

$$E_q = E_q' + (X_d - X_d')i_d$$

该式可用于消去$i_f$($E_q$)。该式同时也是忽略$D$、$Q$绕组时用于表征$E_q$和$E_q'$之间的一个重要关系。

注意：计及$D$、$Q$绕组暂态时，此关系不成立。

$q$轴磁链方程为：

$$\Phi_q = -X_qi_q$$

该式可直接用来消去$\Phi_q$。

至此，消去$\Phi_d$、$\Phi_q$和$i_f$($E_q$)的表达式均已得到，分别为：

$$\Phi_d = E_q - X_di_d$$

$$E_q = E_q' + (X_d - X_d')i_d$$

$$\Phi_q = -X_qi_q$$

导出三阶模型

对原始电压方程，令$p\Phi_d=p\Phi_q=0, \omega \approx 1$，再将$\Phi_d = E_q - X_di_d$和$\Phi_q = -X_qi_q$代入，得

$$\left\{ \begin{aligned} u_d = X_qi_q - r_ai_d \\ u_q = E_q' - X_d'i_d - r_ai_q \end{aligned} \right.$$

对于励磁绕组电压方程，将其改写为

$$p\Phi_f = u_f - r_fi_f$$

上式两侧同乘

$$\frac{X_{ad}}{X_f}\times\frac{X_f}{r_f}$$

由于$T_{d0}'=X_f / r_f$，再由$E_f$、$E_q$和$E_q'$的定义，可得

$$T_{d0}'pE_q'=E_f - E_q$$

将$E_q = E_q' + (X_d - X_d')i_d$代入上式，消去$E_q$，有

$$T_{d0}'pE_q' = E_f - E_q' - (X_d - X_d')i_d$$

上式即为转子励磁绕组的暂态方程。

另对转子运动方程改造如下：

根据

$$T_J \frac{d\omega}{dt} = T_m - T_e = T_m - [E_q'i_q - (X_d' - X_q)i_di_q]$$

消去$\Phi_d$和$\Phi_q$，得到

$$T_J \frac{d\omega}{dt} = T_m - T_e = T_m - [E_q'i_q - (X_d' - X_q)i_di_q]$$

另一运动方程不变，为

$$\frac{d\delta}{dt} = \omega - 1$$

至此，以下四个式子构成了同步发电机的实用三阶模型：

$$\left\{ \begin{aligned} u_d = X_qi_q - r_ai_d \\ u_q = E_q' - X_d'i_d - r_ai_q \end{aligned} \right.$$

$$T_{d0}'pE_q' = E_f - E_q' - (X_d - X_d')i_d$$

$$T_J \frac{d\omega}{dt} = T_m - T_e = T_m - [E_q'i_q - (X_d' - X_q)i_di_q]$$

$$\frac{d\delta}{dt} = \omega - 1$$

推广至十二相同步发电机

十二相同步发电机的定子绕组在一定条件下可视为4个完全解耦的三相同步发电机定子绕组，每套Y绕组之间位移15°电角度。因此三相同步发电机模型和十二相同步发电机模型只在Park变换上有绕组数量和位移的差别，对于定转子分解的计算和分析则完全一致。

对于和$E_q$，可以很简单的推导如下。首先有：

$$T_{d0}'pE_q' = E_f - E_q' - (X_d - X_d')i_d$$

移项为求解$E_q'$形式，并$Laplace$变换至$s$域：

$$E_q' = \frac{1}{T_{d0}'s+1}(E_f-(X_d - X_d')i_d)$$

对于转子运动方程，若原动机为柴油机，在考虑机组摩擦转矩阻尼系数$\lambda_f$的情况下，有

$$T_m - T_e - \lambda_f \omega = T_J \frac{d\omega}{dt}$$

$$\omega = \frac{T_m - T_e}{T_J s + \lambda_f}$$

Simulink模型

对于Simulink模型，机端电压$u_d$和$u_q$为结果量而非驱动量，实际的驱动量为发电机感应电动势$e_d$和$e_q$：

$$e_d = p\Phi_d - \omega\Phi_q$$

$$e_q = p\Phi_q + \omega\Phi_d$$

三阶实用模型中通常忽略定子暂态，即令$p\Phi_d=p\Phi_q=0$，于是有

$$e_d \approx - \omega\Phi_q$$

$$e_q \approx \omega\Phi_d$$

我们已经在之前的推导中得到$\Phi_d$和$\Phi_q$的实用参数表达式

$$\Phi_d = E_q - X_di_d$$

$$\Phi_q = - X_qi_q$$

代入$E_q = X_{ad}i_f$，有

$$\Phi_d = X_{ad}i_f - X_di_d$$

联立，有

$$e_d = \omega X_qi_q$$

$$e_q = \omega X_{ad}i_f - \omega X_di_d$$

上式可用于代数计算某一时刻的$e_d$和$e_q$，但无法反应系统特征。要获取系统特征，改写为以下式子：

$$e_d = \omega X_qi_q$$

$$e_q = \omega E_q' - \omega X_d'i_d = \omega \frac{1}{T_{d0}'s+1}(E_f-(X_d - X_d')i_d) - \omega X_d'i_d$$

励磁系统简化模型

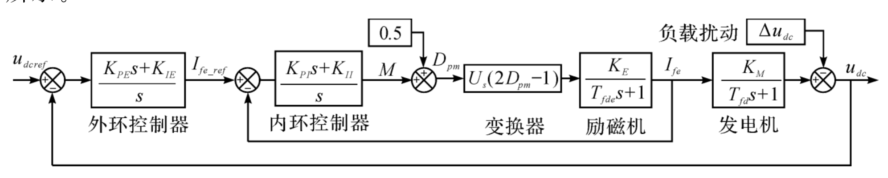
对于励磁系统而言，不考虑饱和、剩磁和转速变化的影响时，主励磁机可简化为一阶惯性环节：

$$G_{E}(s)=\frac{K_E}{T_{fde}s+1}$$

式中，$T_{fde}$为励磁机励磁绕组时间常数，$K_E$为励磁机放大倍数。

事实上，对于电力系统建模而言，励磁机的作用仅仅只是根据输入和参考量，来计算得到合适的$E_f$，因此无需对励磁机本身做非常精确的建模。任何一个电气量(比如$X_{fd}$)的细微差别都可能被控制器抵消。在这种情况下，仅需保证励磁系统结构和输出量正确即可，无需过分关注部分元器件的精确参数。

定转子分解模型

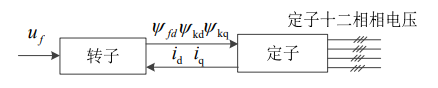
转子模型

计及转子稳定绕组的情况下，考虑转子磁链方程为

$$\left\{ \begin{aligned} p\psi_{fd} &= \omega_b \left( u_{fd} - r_{fd} i_{fd} \right) \\ p\psi_{kd} &= \omega_b \left( - r_{kd} i_{kd} \right) \\ p\psi_{fq} &= \omega_b \left( - r_{fq} i_{fq} \right) \\ p\psi_{kq} &= \omega_b \left( - r_{kq} i_{kq} \right) \end{aligned} \right.$$

式中$\omega_b$为转速基值。标幺化时时间基值为$t_B = 1/\omega_B$，因此对时间的微分实际上为

$$p=\frac{d}{dt^*} = \frac{d}{\omega_B t}$$

由转子磁链方程

$$\left\{ \begin{aligned} \psi_{fd} = \psi_{ad} + \psi_{fdl} \\ \psi_{kd} = \psi_{ad} + \psi_{kdl} \\ \psi_{fq} = \psi_{aq} + \psi_{fql} \\ \psi_{kq} = \psi_{aq} + \psi_{kql} \end{aligned} \right.$$

式中$\psi_{md}$和$\psi_{mq}$为直轴、交轴激磁磁链。

上式可进一步化为适合计算的形式：

$$\left\{ \begin{aligned} i_{fd} = x_{fdl}^{-1}(\psi_{fd} - \psi_{ad}) \\ i_{kd} = x_{kdl}^{-1}(\psi_{kd} - \psi_{ad}) \\ i_{fq} = x_{fql}^{-1}(\psi_{fq} - \psi_{aq}) \\ i_{kq} = x_{kql}^{-1}(\psi_{kq} - \psi_{aq}) \end{aligned} \right.$$

根据磁路基尔霍夫定理，直轴、交轴激磁磁链不计饱和时的计算公式为

$$\left\{ \begin{aligned} \frac{\psi_{ad}}{x_{ad}'} = -\Sigma i_{di} + \frac{\psi_{fd}}{x_{fdl}} + \frac{\psi_{kd}}{x_{kdl}} \\ \frac{\psi_{aq}}{x_{aq}'} = -\Sigma i_{qi} + \frac{\psi_{fq}}{x_{fql}} + \frac{\psi_{kq}}{x_{kql}} \end{aligned} \right.$$

整理有

$$\left\{ \begin{aligned} \psi_{ad} = x_{ad}'(-(i_{d1}+i_{d2}+i_{d3}+i_{d4}) + \frac{\psi_{fd}}{x_{fdl}} + \frac{\psi_{kd}}{x_{kdl}}) \\ \psi_{aq} = x_{aq}'(-(i_{q1}+i_{q2}+i_{q3}+i_{q4}) + \frac{\psi_{fq}}{x_{fql}} + \frac{\psi_{kq}}{x_{kql}}) \end{aligned} \right.$$

式中$x_{ad}'$和$x_{aq}'$由等效感抗合成得来：

$$\left\{ \begin{aligned} x_{ad}' = x_{fdl} // x_{kdl} // x_{ad} \\ x_{aq}' = x_{fql} // x_{kql} // x_{aq} \end{aligned} \right.$$

上面两个式子可以求解得到转子激磁磁链。

定子模型

直轴部分

首先引入实用变量$x_d''$:

$$x_d'' = x_{ls} + x_{ad} // x_{fdl} // x_{kdl}$$

并且

$$x_{fd} = x_{fdl} + x_{ad}, \quad x_{kd} = x_{kdl} + x_{ad}$$

定义$q$轴超瞬变电动势$E_q''$，其物理意义时当$fd$绕组磁链为$\psi_{fd}$，$kd$绕组磁链为$\psi_{kd}$时，同步转速下的定子$q$轴开路电动势。

根据叠加原理，同步转速下时，有：

$$\psi_d = \frac{\psi_{fd}}{x_{fdl} + x_{ad} // x_{kdl}} \times \frac{x_{kdl}}{x_{ad} + x_{kdl}} \times x_{ad} + \frac{\psi_{kd}}{x_{kdl} + x_{ad} // x_{fdl}} \times \frac{x_{fdl}}{x_{ad} + x_{fdl}} \times x_{ad} \\ = \frac{x_{ad}}{x_{fd}x_{kd} - x_{ad}^2}(x_{kdl}\psi_{fd} + x_{fdl}\psi_{kd})$$

同步转速下电机定子开路时，$E_q''$的值即等于$\psi_d$为

$$E_q'' = \frac{x_{ad}}{x_{fd}x_{kd} - x_{ad}^2}(x_{kdl}\psi_{fd} + x_{fdl}\psi_{kd})$$

根据同步发电机五阶实用模型，$d$轴磁链表达式为

$$\psi_d = E_q'' - X_d''i_d \\ = \frac{x_{ad}}{x_{fd}x_{kd} - x_{ad}^2}(x_{kdl}\psi_{fd} + x_{fdl}\psi_{kd}) - X_d''i_d$$

考虑将上式等号右侧的分式项转换成带漏抗的形式。展开分母，有

$$\begin{aligned} x_{fd} \cdot x_{kd} - x_{ad}^2 &= (x_{fdl} + x_{ad})(x_{kdl} + x_{ad}) - x_{ad}^2 \\ &= x_{fdl} x_{kdl} + x_{fdl} x_{ad} + x_{ad} x_{kdl} + x_{ad}^2 - x_{ad}^2 \\ &= x_{fdl} x_{kdl} + x_{fdl} x_{ad} + x_{ad} x_{kdl} \end{aligned}$$

因此原分式可以改写为

$$\frac{x_{ad}}{x_{fd} \cdot x_{kd} - x_{ad}^2} = \frac{x_{ad}}{x_{fdl} x_{kdl} + x_{ad} x_{kdl} + x_{ad} x_{fdl}}$$

因此原式子等号右侧可以改写为：

$$\frac{x_{ad}}{x_{fdl} x_{kdl} + x_{ad} x_{kdl} + x_{ad} x_{fdl}} \cdot x_{kdl} \cdot \psi_{fd} + \frac{x_{ad}}{x_{fdl} x_{kdl} + x_{ad} x_{kdl} + x_{ad} x_{fdl}} \cdot x_{fdl} \cdot \psi_{kd}$$

我们恰好有

$$x_{ad}' = x_{ad} \parallel x_{fdl} \parallel x_{kdl} = \frac{x_{ad} \cdot x_{fdl} \cdot x_{kdl}}{x_{fdl} x_{kdl} + x_{ad} x_{kdl} + x_{ad} x_{fdl}}$$

显然能够得到以下关系式：

$$\frac{x_{ad}}{x_{fd} \cdot x_{kd} - x_{ad}^2} \cdot x_{kdl} = \frac{x_{ad} \cdot x_{fdl} \cdot x_{kdl}}{x_{fdl} x_{kdl} + x_{ad} x_{kdl} + x_{ad} x_{fdl}} =\frac{x_{ad}'}{x_{fdl}} \cdot \frac{1}{x_{fdl}}\\ \frac{x_{ad}}{x_{fd} \cdot x_{kd} - x_{ad}^2} \cdot x_{fdl} = \frac{x_{ad} \cdot x_{fdl} \cdot x_{kdl}}{x_{fdl} x_{kdl} + x_{ad} x_{kdl} + x_{ad} x_{fdl}} = \frac{x_{ad}'}{x_{fdl}} \cdot \frac{1}{x_{kdl}}$$

因此原式子可以改写为

$$\psi_d = -x_d''i_d + \frac{x_{ad}'}{x_{fdl}}\psi_{fd} + \frac{x_{ad}'}{x_{kdl}}\psi_{kd}$$

交轴部分

同理，可得到

$$\psi_q = -x_q''i_q + \frac{x_{aq}'}{x_{fql}}\psi_{fq} + \frac{x_{aq}'}{x_{kql}}\psi_{kq}$$

最终形式

联立直轴和交轴方程，得到

$$\psi_d = -x_d''i_d + \frac{x_{ad}'}{x_{fdl}}\psi_{fd} + \frac{x_{ad}'}{x_{kdl}}\psi_{kd} \\ \psi_q = -x_q''i_q + \frac{x_{aq}'}{x_{fql}}\psi_{fq} + \frac{x_{aq}'}{x_{kql}}\psi_{kq}$$

其中

$$x_d'' = x_{ls} + x_{ad} // x_{fdl} // x_{kdl} = x_{ls} + x_{ad}'\\ x_q '' = x_{ls} + x_{aq} // x_{fql} // x_{kql} = x_{ls} + x_{aq}'\\ x_{ad}' = x_{ad} // x_{fdl} // x_{kdl} \\ x_{aq}' = x_{aq} // x_{fql} // x_{kql} \\$$

已知电压方程为

$$u_d = p\psi_d - \omega\psi_q - r_ai_d \\ u_q = p\psi_q + \omega\psi_d - r_ai_q \\$$

将磁链方程代入到电压方程，可得

$$\begin{aligned} u_d = & - (x_d'' p + r_a) i_d + \omega x_q'' i_q + \frac{x_{ad}'}{x_{fdl}} p\psi_{fd} + \frac{x_{ad}'}{x_{kdl}} p\psi_{kd} - \omega \frac{x_{aq}'}{x_{fql}} \psi_{fq} - \omega \frac{x_{aq}'}{x_{kql}} \psi_{kq} \\ \\ u_q = & - (x_q'' p + r_a) i_q - \omega x_d'' i_d + \frac{x_{aq}'}{x_{fql}} p\psi_{fq} + \frac{x_{aq}'}{x_{kql}} p\psi_{kq} + \omega \frac{x_{ad}'}{x_{fdl}} \psi_{fd} + \omega \frac{x_{ad}'}{x_{kdl}} \psi_{kd} \end{aligned}$$

将其改写为更简洁的形式：

$$u_d = -x_d''pi_d + \omega x_q''i_q + (\frac{x_{ad}'}{x_{fdl}} p\psi_{fd} + \frac{x_{ad}'}{x_{kdl}} p\psi_{kd} - \omega \frac{x_{aq}'}{x_{fql}} \psi_{fq} - \omega \frac{x_{aq}'}{x_{kql}} \psi_{kq}) - r_ai_d \\ u_q = -x_q''pi_q - \omega x_d''i_d + (\frac{x_{aq}'}{x_{fql}} p\psi_{fq} + \frac{x_{aq}'}{x_{kql}} p\psi_{kq} + \omega \frac{x_{ad}'}{x_{fdl}} \psi_{fd} + \omega \frac{x_{ad}'}{x_{kdl}} \psi_{kd}) - r_ai_q$$

括号内的式子实际上就是$e_d''$和$e_q''$：

$$e_d'' = \frac{x_{ad}'}{x_{fdl}} p\psi_{fd} + \frac{x_{ad}'}{x_{kdl}} p\psi_{kd} - \omega \frac{x_{aq}'}{x_{fql}} \psi_{fq} - \omega \frac{x_{aq}'}{x_{kql}} \psi_{kq} \\ e_q'' = \frac{x_{aq}'}{x_{fql}} p\psi_{fq} + \frac{x_{aq}'}{x_{kql}} p\psi_{kq} + \omega \frac{x_{ad}'}{x_{fdl}} \psi_{fd} + \omega \frac{x_{ad}'}{x_{kdl}} \psi_{kd} \\$$

定子电压方程可简化为

$$u_d = e_d'' -x_d''pi_d + \omega x_q''i_q - r_ai_d \\ u_q = e_q'' -x_q''pi_q - \omega x_d''i_d - r_ai_q$$

等效三相电抗对称$(x_d''=x_q'')$的前提下，对上式作Park逆变换，有

$$\left\{ \begin{aligned} u_a = e_a'' - L_d''\frac{di_a}{dt} - r_ai_a \\ u_b = e_b'' - L_d''\frac{di_b}{dt} - r_ai_b \\ u_c = e_c'' - L_d''\frac{di_c}{dt} - r_ai_c\\ \end{aligned} \right.$$

上式即为标准电动势-机端电压表达式。$L_d''$和$r_a$可用Powergui电感和电阻模拟。

等式成立需要满足条件$x_d''=x_q''$，通常情况下二者并不严格相等，为了解决此问题，文献[40]提出了在$q$轴转子侧加一虚拟阻尼电阻的方法，从而令$x_d''=x_q''$，并且通过仿真验证了新添加的虚拟阻尼电阻并不会显著影响转子暂态性能。

励磁控制器参数设计

不考虑饱和、剩磁和转速变化的情况下，主励磁机可简化为一阶惯性环节

$$G_E(s) = \frac{K_E}{T_{fde}s+1}$$

式中$T_{fde}$为励磁机时间常数。

励磁机内环（励磁电流内环）控制器传递函数为

$$G_I(s) = K_{PI} + \frac{K_{II}}{s} = \frac{K_{PI}s+K_{II}}{s}$$

直流电压外环控制器传递函数为

$$G_E(s) = K_{PE} + \frac{K_{IE}}{s} = \frac{K_{PE}s+K_{IE}}{s}$$

励磁机励磁内环控制系统开环传递函数为

$$G_K(s) = \frac{2K_{II}(\frac{K_{PI}}{K_{II}}s+1)}{s}\frac{1}{T_{fde}s+1}$$

为简化设计，可选择内环控制器PI参数来对消励磁机惯性环节以降低系统阶数，即

$$\frac{K_{PI}}{K_{II}} = T_{fde} = 0.06s$$