RNN：原理、组成与简单实现

传统RNN

循环神经网络（RNN）最早可以追溯到1980年代末，当时的研究者希望设计一种能够处理时间序列数据或具有时序依赖关系的数据的神经网络模型。RNN的设计灵感来自生物神经网络的工作原理，它模拟了大脑神经元的反馈机制，通过递归连接来捕捉数据中前后时刻的依赖关系。

历史

RNN的初期发展可追溯到1986年，David Rumelhart 和 Geoffrey Hinton 等人提出了反向传播算法，并在此基础上构建了简单的RNN模型。最初的RNN能够通过训练学习输入数据的时序模式。RNN 跟传统神经网络最大的区别在于每次都会将前一次的输出结果，带到下一次的隐藏层中，一起训练。

工作原理

以一个最简单的语序为例：用户输入了一句“what time is it”，首先需要对这句话进行分词：

第一步：分词

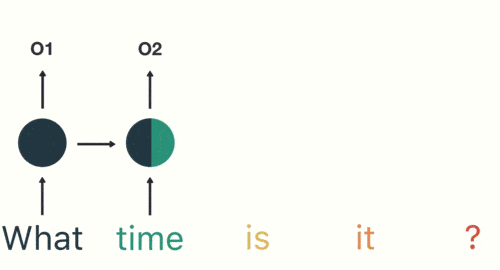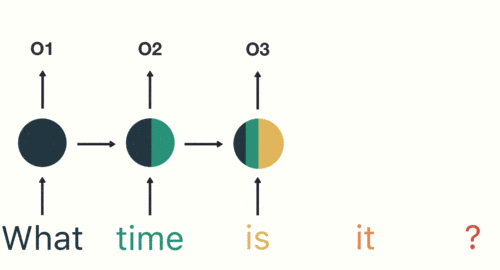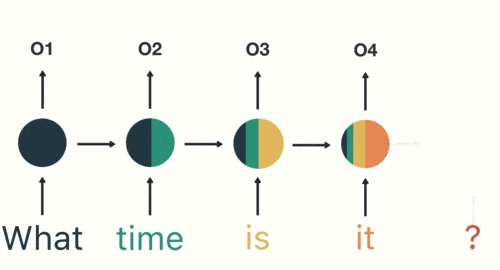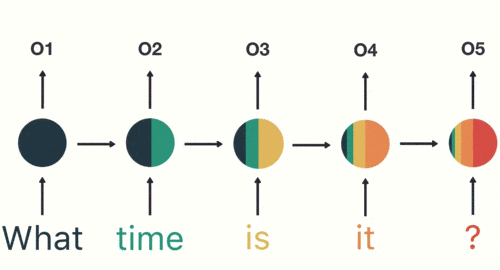
将分词结果按顺序输入RNN。首先输入“what”：

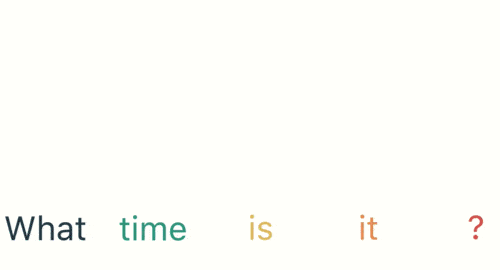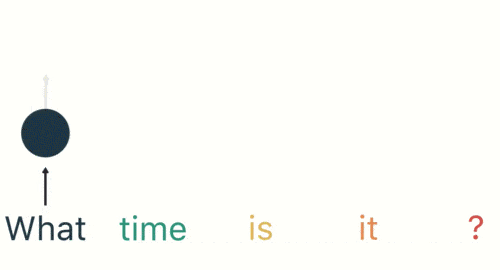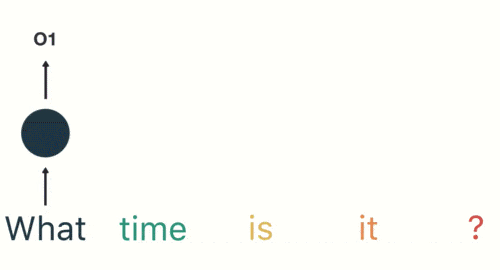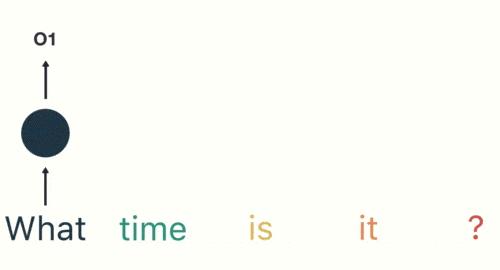
第二步：输入"what"

按顺序输入剩下的分词，第三步输入“time”。按照RNN的结构，输入"time"时，之前输入的"what"会对RNN的输出产生影响（隐藏层中有一半是黑色的）

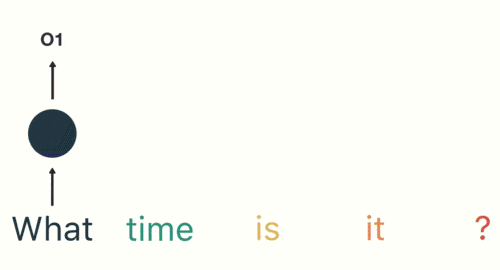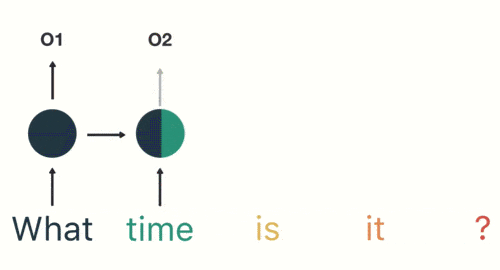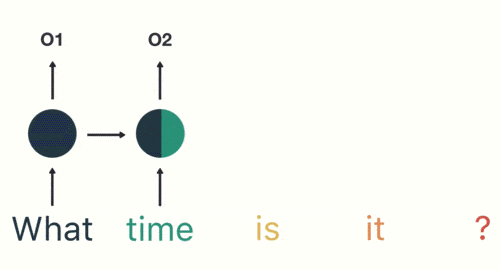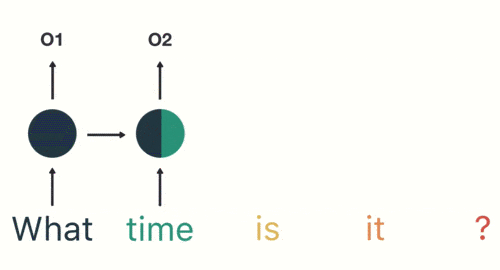
第三步：输入"time"

以此类推，每一个历史输入都会对未来输出产生影响，直观显示为每一个圆形隐藏层中都包含了之前所有历史输入所指代的颜色。

第四步：历史输入会影响未来输出

最后需要输出结果（此处是判断这句话的意图）时，只需要输出最后一层的结果。

组成和基本结构

RNN的核心组成部分是循环结构，它使得网络能够记住之前时刻的信息，并通过这种“记忆”来影响当前时刻的计算。RNN的基本结构可以通过以下几个部分来理解：

1. 输入层（Input Layer）

输入序列数据，通常表示为一个时间步的输入向量 $ x_t $。例如，在自然语言处理任务中，输入可以是一个词向量；在时间序列预测任务中，输入可以是某一时刻的传感器数据。

2. 隐层（Hidden Layer）

隐藏层由多个神经元组成，每个神经元的输出不仅受到当前输入的影响，还受到前一时刻隐层状态的影响。该层的计算过程可以表示为：

h_t = f(W_{xh}x_t + W_{hh}h_{t-1} + b_h)

其中，$ h_t $ 是当前时刻的隐层状态，$ x_t $ 是当前输入，$ h_{t-1} $ 是前一时刻的隐层状态，$ W_{xh} $ 和 $W_{hh} $ 是权重矩阵，$ b_h $ 是偏置项，$ f $ 是激活函数（如tanh或ReLU）。

3. 输出层（Output Layer）

输出层用于生成预测结果，通常可以表示为：

y_t = g(W_{hy}h_t + b_y)

其中，$ y_t $ 是当前时刻的输出，$ W_{hy} $ 是从隐层到输出的权重矩阵，$ b_y $ 是输出层的偏置项，$ g $ 是输出的激活函数（例如softmax或sigmoid，取决于任务）。

应用

RNN在时间序列数据处理中的优势是能够捕捉时间序列的动态变化和时序依赖关系，因此它特别适用于处理和预测具有时序特征的数据。

RNN的缺点也很明显，即短期的记忆影响较大，长期的记忆影响较小。若整个时间序列非常长，RNN甚至可能丢失很久之前的历史输入。同时，训练RNN也需要大量的成本，并且很容易带来梯度消失和梯度爆炸问题。这就引出了后来的变种：门控循环单元（GRU）与长短期记忆网络（LSTM）。

门控循环单元（GRU）

参考文献：Cho, K., Van Merriënboer, B., Bahdanau, D., & Bengio, Y. (2014). On the properties of neural machine translation: encoder-decoder approaches. arXiv preprint arXiv:1409.1259.

来源

GRU被用于解决传统RNN的梯度异常问题。这种梯度异常问题在序列问题中是非常常见的，比如：

早期观测值对预测所有未来观测值具有非常重要的意义。考虑一个极端情况，其中第一个观测值包含一个校验和，目标是在序列的末尾辨别校验和是否正确。在这种情况下，第一个词元的影响至关重要。我们希望有某些机制能够在一个记忆元里存储重要的早期信息。如果没有这样的机制，我们将不得不给这个观测值指定一个非常大的梯度，因为它会影响所有后续的观测值。
一些特征或现象没有相关的观测值。例如，在对网页内容进行情感分析时，可能有一些辅助HTML代码与网页传达的情绪无关。我们希望有一些机制来跳过隐状态表示中的此类词元。
序列的各个部分之间存在逻辑中断。例如，书的章节之间可能会有过渡存在，或者证券的熊市和牛市之间可能会有过渡存在。在这种情况下，最好有一种方法来重置我们的内部状态表示。

工作原理

GRU与传统RNN的关键区别在于，GRU支持隐状态的门控。这意味着模型有专门的机制来确定应该何时更新隐状态，以及应该何时重置隐状态。这些机制是可学习的，并且能够解决了上面列出的问题。例如，如果第一个序列数据变化现象非常重要（如发电机故障中匝间短路的那一瞬间），模型将学会在第一次观测之后不更新隐状态。同样，模型也可以学会跳过不相关的临时观测。最后，模型还将学会在需要的时候重置隐状态。

重置门（Reset Gate）

重置门用于决定当前时刻的输入数据在计算当前状态时对之前状态的影响程度。即它决定在计算新的候选隐藏状态时，前一时刻的隐层状态应该有多大的影响。

公式表示为：

r_t = \sigma(W_r x_t + U_r h_{t-1} + b_r)

其中， $r_t$ 是重置门的输出， $W_r$ 和 $U_r$ 是权重矩阵， $x_t$ 是当前时刻的输入， $h_{t-1}$ 是前一时刻的隐藏状态， $b_r$ 是偏置项， $\sigma$ 是sigmoid激活函数。

当 $r_t$ 接近0时，表示前一时刻的隐藏状态对当前时刻的影响很小，网络将“重置”之前的记忆。

更新门（Update Gate）

更新门控制着当前时刻的隐藏状态应该如何更新，它决定了当前时刻的输出应保留多少来自上一时刻的状态，多少来自当前输入的候选隐藏状态。更新门的值接近1时，意味着当前时刻的隐藏状态保留更多来自前一时刻的记忆；而接近0时，意味着更多的依赖于当前输入。

公式表示为：

z_t = \sigma(W_z x_t + U_z h_{t-1} + b_z)

其中， $z_t$ 是更新门的输出， $W_z$ 和 $U_z$ 是权重矩阵， $x_t$ 是当前时刻的输入， $h_{t-1}$ 是前一时刻的隐藏状态， $b_z$ 是偏置项。

GRU中计算重置门和更新门

候选隐藏状态（Candidate Hidden State）

候选隐藏状态是GRU网络根据当前输入和重置门的作用计算出来的，表示网络在当前时刻希望更新的“记忆”。它是基于当前输入和前一时刻的记忆状态计算的。

公式表示为：

\tilde{h}_t = \tanh(W_h x_t + U_h (r_t \cdot h_{t-1}) + b_h)

其中， $\tilde{h}_t$ 是候选隐藏状态， $W_h$ 和 $U_h$ 是权重矩阵， $r_t$ 是重置门的输出， $\cdot$ 表示按元素相乘（Hadamard积）， $\tanh$ 是tanh激活函数。

GRU中计算候选隐藏状态

最终隐藏状态（Final Hidden State）

最终的隐藏状态是当前时刻候选隐藏状态和上一时刻的隐藏状态的加权平均。加权系数由更新门 $z_t$ 控制，表示信息应该更新多少，保留多少。

公式表示为：

h_t = (1 - z_t) \cdot \tilde{h}_t + z_t \cdot h_{t-1}

其中， $h_t$ 是当前时刻的最终隐藏状态， $\tilde{h}_t$ 是候选隐藏状态， $z_t$ 是更新门， $h_{t-1}$ 是前一时刻的隐藏状态。

GRU中计算最终隐藏状态

简单应用

GRU十分适合用于时间序列数据的特征识别、提取和预测，尤其是较长时间内的时间序列。
下面是一个用于预测未来一段时间内天气状况的模型，其使用五个GRU层，用于对四个不同变量（最高温、最低温、降水量与风速）进行回归任务。数据集来自于Kaggle

import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input, GRU, Dense, Dropout
import tensorflow.keras.backend as K
import matplotlib.pyplot as plt

# 1. 加载CSV文件，读取日期数据，并转换为日期格式
df = pd.read_csv('seattle-weather.csv', parse_dates=['date'])

# 2. 处理缺失值，使用前向填充（前一个有效值填充）
df.fillna(method='ffill', inplace=True)

# 3. 规范化数值特征
# 使用 MinMaxScaler 将数据缩放到 0 和 1 之间
scaler = MinMaxScaler()
scaled_features = ['precipitation', 'temp_max', 'temp_min', 'wind']  # 需要规范化的特征
df[scaled_features] = scaler.fit_transform(df[scaled_features])

# 4. 创建时间序列数据：输入X是过去window_size天的特征，y是目标列（temp_max, temp_min, precipitation, wind）
def create_sequences(df, window_size, target_columns):
    X, y = [], []
    for i in range(len(df) - window_size):
        # 过去 window_size 天的数据作为输入
        X.append(df.iloc[i:i + window_size][scaled_features].values)
        # 当前天的目标特征作为输出
        y.append(df.iloc[i + window_size][target_columns].values)  # 多目标回归
    return np.array(X), np.array(y)

# 设置时间窗口为15天，目标列为气温、降水量和风速
window_size = 15
target_columns = ['temp_max', 'temp_min', 'precipitation', 'wind']  # 目标列：温度、降水量和风速
X, y = create_sequences(df, window_size, target_columns)

# 5. 划分训练集和测试集，采用80%的数据用于训练，20%用于测试
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, shuffle=False)

# 6. 转换数据格式
X_train, y_train = np.array(X_train), np.array(y_train)
X_test, y_test = np.array(X_test), np.array(y_test)

# 将目标值数据类型转换为 float32，以便模型训练
y_train = y_train.astype(np.float32)
y_test = y_test.astype(np.float32)

# 输出训练集和测试集的形状，确保数据格式正确
print("X_train shape:", X_train.shape)
print("X_test shape:", X_test.shape)
print("y_train shape:", y_train.shape)
print("y_test shape:", y_test.shape)

# 7. 构建共享底层GRU网络 + 多目标回归模型

# 输入层，形状为 (window_size, 4)，即过去15天的4个特征
input_layer = Input(shape=(window_size, len(scaled_features)))

# 构建多层GRU网络，每层后面都添加Dropout层，以防止过拟合
x = GRU(256, return_sequences=True)(input_layer)  # 第1层GRU，返回所有时间步的输出
x = Dropout(0.2)(x)  # Dropout，丢弃20%的神经元

x = GRU(256, return_sequences=True)(x)  # 第2层
x = Dropout(0.2)(x)  # Dropout

x = GRU(128, return_sequences=True)(x)  # 第3层
x = Dropout(0.2)(x)  # Dropout

x = GRU(128, return_sequences=True)(x)  # 第4层
x = Dropout(0.2)(x)  # Dropout

x = GRU(64)(x)  # 第5层，只返回最后一个时间步的输出
x = Dropout(0.2)(x)  # Dropout

# 4个目标列的独立输出层，每个输出层预测一个目标
temp_max_output = Dense(1, name='temp_max')(x)  # 输出温度最大值
temp_min_output = Dense(1, name='temp_min')(x)  # 输出温度最小值
precipitation_output = Dense(1, name='precipitation')(x)  # 输出降水量
wind_output = Dense(1, name='wind')(x)  # 输出风速

# 定义模型，输入为输入层，输出为4个目标特征
model = Model(inputs=input_layer, outputs=[temp_max_output, temp_min_output, precipitation_output, wind_output])

# 8. 编译模型

# 定义加权损失函数
def weighted_loss(y_true, y_pred):
    # 为每个目标特征设置权重
    temp_max_weight = 1.0
    temp_min_weight = 1.0
    precipitation_weight = 10.0  # 为降水增加权重
    wind_weight = 50.0  # 为风速增加权重

    # 计算加权的损失
    loss = K.mean(K.square(y_true - y_pred), axis=-1)  # 计算均方误差
    weights = K.constant([temp_max_weight, temp_min_weight, precipitation_weight, wind_weight])

    return K.mean(loss * weights, axis=-1)  # 计算加权后的损失

# 编译模型，使用Adam优化器和均方误差作为损失函数
model.compile(optimizer='adam',
              loss='mean_squared_error',  # 对每个输出使用均方误差
              metrics={  # 为每个目标列定义MAE和MSE指标
                  'temp_max': ['mae', 'mse'],         # 针对 temp_max 输出定义 MAE 和 MSE
                  'temp_min': ['mae', 'mse'],         # 针对 temp_min 输出定义 MAE 和 MSE
                  'precipitation': ['mae', 'mse'],    # 针对 precipitation 输出定义 MAE 和 MSE
                  'wind': ['mae', 'mse']              # 针对 wind 输出定义 MAE 和 MSE
              })

# 9. 训练模型
history = model.fit(X_train, [y_train[:, 0], y_train[:, 1], y_train[:, 2], y_train[:, 3]],
                    epochs=150, batch_size=32,  # 设置训练的轮次和每批次的样本数
                    validation_data=(X_test, [y_test[:, 0], y_test[:, 1], y_test[:, 2], y_test[:, 3]]))  # 验证集数据

# 10. 模型评估，返回损失值和每个目标特征的评估指标
results = model.evaluate(X_test, [y_test[:, 0], y_test[:, 1], y_test[:, 2], y_test[:, 3]])

# results 返回的是一个列表，包含了损失值和各个目标特征的MAE和MSE
test_loss = results[0]
test_mae_temp_max = results[2]  # temp_max 对应的 MAE
test_mae_temp_min = results[4]  # temp_min 对应的 MAE
test_mae_precipitation = results[6]  # precipitation 对应的 MAE
test_mae_wind = results[8]  # wind 对应的 MAE

# 输出评估结果
print(f'Test Loss (MSE): {test_loss:.4f}')
print(f'Test MAE for temp_max: {test_mae_temp_max:.4f}')
print(f'Test MAE for temp_min: {test_mae_temp_min:.4f}')
print(f'Test MAE for precipitation: {test_mae_precipitation:.4f}')
print(f'Test MAE for wind: {test_mae_wind:.4f}')

# 11. 可视化训练过程
plt.figure(figsize=(12, 6))

# 绘制总体 Loss（MSE）
plt.subplot(1, 2, 1)
plt.plot(history.history['loss'], label='Train Loss')
plt.plot(history.history['val_loss'], label='Val Loss')
plt.title('Model Loss (MSE)')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()

# 绘制每个输出的 MAE
plt.subplot(1, 2, 2)
plt.plot(history.history['temp_max_mae'], label='Train temp_max MAE')
plt.plot(history.history['val_temp_max_mae'], label='Val temp_max MAE')
plt.plot(history.history['temp_min_mae'], label='Train temp_min MAE')
plt.plot(history.history['val_temp_min_mae'], label='Val temp_min MAE')
plt.plot(history.history['precipitation_mae'], label='Train precipitation MAE')
plt.plot(history.history['val_precipitation_mae'], label='Val precipitation MAE')
plt.plot(history.history['wind_mae'], label='Train wind MAE')
plt.plot(history.history['val_wind_mae'], label='Val wind MAE')

这个模型本质上执行了一个多变量回归任务，其中引入了weighted_loss函数，其通过为每个目标特征设置不同的权重，调整它们在总损失中的影响力，使得模型在训练时能够更加关注某些特征的预测准确性。这对于多目标回归任务尤为重要，特别是在特征的重要性或尺度差异较大的情况下，有助于提高模型的预测性能。

模型在经过粗略调试之后输出了以下结果：

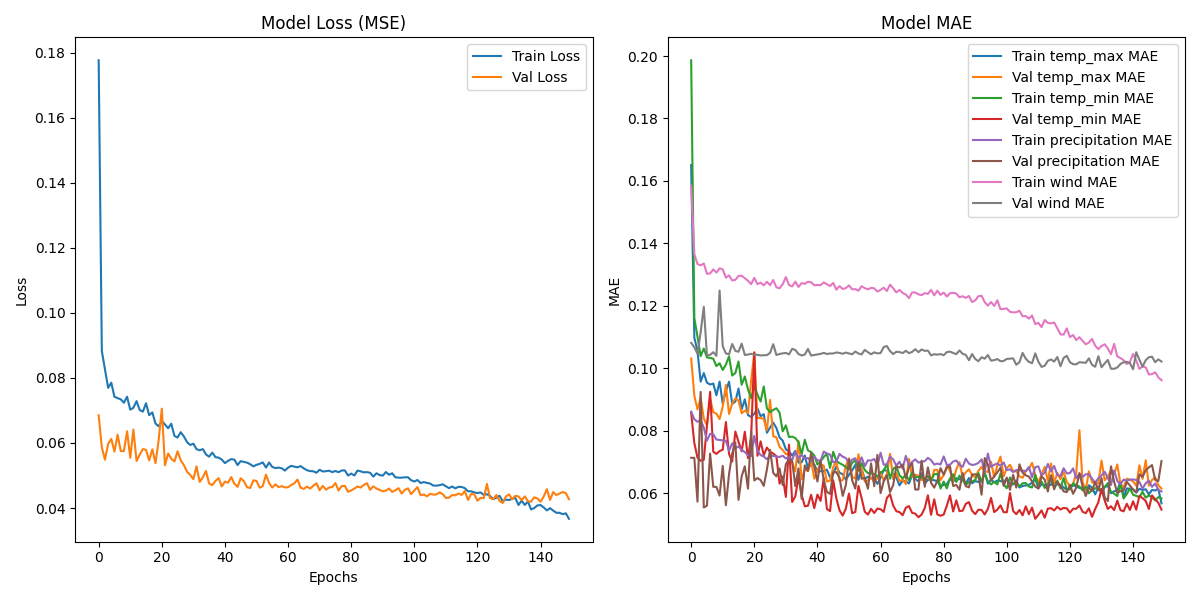
MSE和MAE指标随迭代次数变化

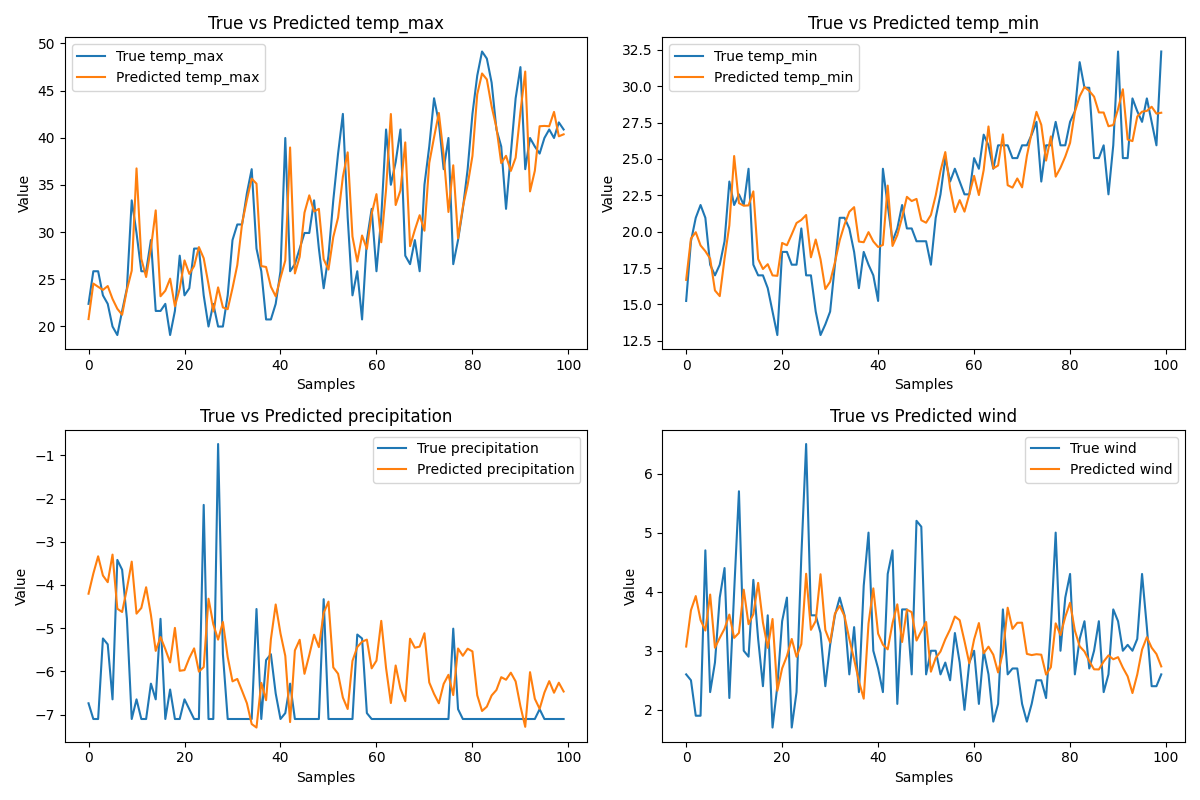
预测结果与实际结果对比

可以看出对于最高气温和最低气温，模型给出了非常好的结果。这也跟GRU的特性有关，因为其能尽可能多地捕捉到变量与时间的关系。而对于那些变化和时间不呈非常明显关系的变量————比如降水量和风速————模型给出的结果并不是非常尽人意，即使这两个变量已经被添加了相当高的权重。尤其是降水量，其突变次数和趋势明显高于其他几个变量，模型也无法做出比较好的计算结果。

这只是一个非常简单的应用，如果结合其他方法，预测准确度应当能达到一个比较高的值。

深度学习

RNN：原理、组成与简单实现

http://akichen891.github.io/2024/12/12/RNN：原理、组成与简单实现/

作者

Aki Chen

发布于

2024年12月12日

更新于

2024年12月12日

许可协议

STM32中的I2C通信下一篇