【电机瞬态分析】交流电机的运算电抗、等效电路、电磁转矩

同步电机等效运算电路

在进行瞬态分析时，亦可根据导出的方程式画出相应的等效电路，这样比较直观也便于记忆。一般情况下，最关心的是电枢绕组各量的变化，即从电枢绕组的端点看，能反映瞬态方程式的等效电路和等效阻抗。通过从a、b、c坐标系统到d、q、0坐标系统的变换，将电感系数从变系数变为了常系数，并通过各基值的选取，使互感系数的标么值可逆，且$L_{ad}=M_{af}=M_{aD}=x_{ad}$，这样就在电路上无联系的几个绕组具备了等效为一个电路的基本条件。当转子转速$\omega$=恒值时，电压方程式为常系数线性微分方程组，可采用拉氏变换将时域的微分方程转换为复频域的代数方程求解。

下面就转子上只有励磁绕组和同时存在励磁和阻尼绕组两种情况，分别对电枢直轴链和交轴磁链的等效运算电路进行讨论。

转子上只有励磁绕组时的等效运算电路

该情况下，根据上篇文章的内容，由标幺值下交流电机方程式推导可得（磁链关系代入电压方程式），直轴电枢磁链方程和励磁绕组电压方程为

$$\psi_d=x_di_d+x_{ad}i_f$$

$$u_f=px_{ad}i_d+(r_f+px_f)i_f$$

式中$p$为时间微分算子。可见各变量为时间的函数，相应的方程为微分方程。当电流$i_d、i_f$的初值为零时，拉氏变换后方程的形式不变，但$p$为一代数复变量，各变量是以$p$为变量的变换函数，如变量$\psi、i、u$经拉氏变换后分别用$\psi(p)、I(p)、U(p)$表示，以示区别。如此改写后的磁链和电压方程式的变换函数为

$$u_d(p)=x_dI_d(p)+x_{ad}I_f(p)$$

$$U_f(p)=px_{ad}I_d(p)+(r_f+px_f)I_f(p)$$

注意：此处的$p$在代数学意义上可视为拉普拉斯变换算子$s$。$U(p)$即等同于$U(s)$，从$U(t)$经$Laplace$变换而来。

用$p$除等式$U_f(p)$两端，并考虑到$x_d=x_l+x_{ad}$，$x_f=x_{fl}+x_{ad}$，整理后可得

$$\psi_d(p)=x_lI_d(p)+x_{ad}[I_d(p)+I_f(p)]$$

$$\frac{U_f(p)}{p}=x_{ad}[I_d(p)+I_f(p)]+(x_{fl}+\frac{r_f}{p})I_f(p)$$

根据上式即可画出相应的直轴等效运算电路，如下图所示。

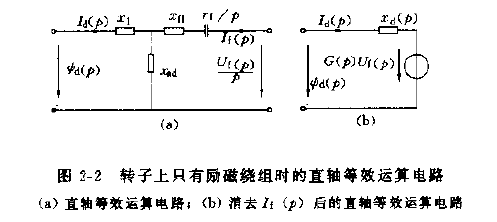
在多数情况下只需研究定子上的各变量，因而可以将等式中的转子电流项$I_f(p)$消去，以获得更加简明的关系式。应用戴维南定理，根据图(a)，得到开路电压$G(p)U_f(p)$及短路阻抗$x_d(p)$，即

$$\psi_d(p)=G(p)U_f(p)+x_d(p)I_d(p)$$

式中

$$G_(p)=\frac{x_{ad}}{r_f+x_fp}$$

$$x_d(p)=x_l+\frac{1}{\frac{1}{x_{ad}+\frac{1}{x_{fl}+\frac{r_f}{p}}}}$$

式中$G_(p)$称为励磁电压对直轴磁链的传递函数，$x_d(p)$称为直轴运算电抗。二者都是具有恒系数的运算式，和电机瞬时转速无关，因而可以用来研究任意转速下电机的各种运行工况。

转子上有励磁绕组、D轴阻尼绕组和Q轴阻尼绕组

直轴等效运算电路

当转子直轴上除励磁绕组外还装有短路的阻尼绕组，且当各绕组电流初值为零时，可得到直轴电枢绕组磁链方程和励磁绕组、直轴阻尼绕组电压方程式的变换函数方程为

$$\psi_d(p)=x_dI_d(p)+x_{ad}I_f(p)+x_{ad}I_D(p)$$

$$U_f(p)=px_{ad}I_d(p)+(r_f+px_f)I_f(p)+px_{ad}I_D(p)$$

$$0=px_{ad}I_d(p)+px_{ad}I_f(p)+(r_D+px_D)I_D(p)$$

用$p$除以等式两侧，考虑$x_d=x_l+x_{ad}$，$x_f=x_{fl}+x_{ad}$，$x_D=x_{Dl}+x_{ad}$，整理后有

$$\psi_d(p)=x_lI_d(p)+x_{ad}[I_d(p)+I_f(p)+I_D(p)]$$

$$\frac{U_f(p)}{p}=x_{ad}[I_d(p)+I_f(p)+I_D(p)]+(x_{fl}+\frac{r_f}{p})I_f(p)$$

$$0=x_{ad}[I_d(p)+I_f(p)+I_D(p)]+(x_{Dl}+\frac{r_D}{p})I_D(p)$$

根据上式，导出得有阻尼绕组时得直轴等效运算电路

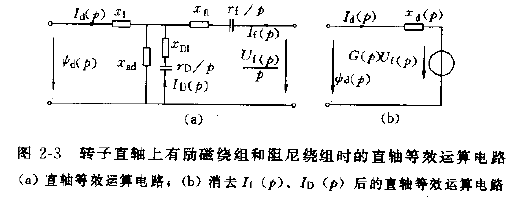
根据戴维南定理，可得开路电压$G(p)U_f(p)$及短路阻抗$x_d(p)$，则$\psi_d(p)$为

$$\psi_d(p)=G(p)U_f(p)+x_d(p)I_d(p)$$

其中

$$G(p)=\frac{(x_Dx_{ad}-x_{ad}^2)p+x_{ad}r_D}{(x_fx_D-x_{ad}^2)p^2+(x_fr_D+x_Dr_f)p+r_fr_D}$$

$$x_d(p)=x_l+\frac{1}{\frac{1}{x_{ad}}+\frac{1}{x_{fl}+\frac{r_f}{p}}+\frac{1}{x_{Dl}+\frac{r_D}{p}}}$$

交轴等效运算电路

转子交轴上有短路的阻尼绕组，且各绕组电流初值为零时，可得到交轴电枢绕组磁链方程和交轴阻尼绕组电压方程式的变换函数为

$$\psi_q(p)=x_qI_q(p)+x_{aq}I_Q(p)$$

$$0=x_{aq}I_q(p)+(x_Q+\frac{r_Q}{p})I_Q(p)$$

类似于直轴情况，考虑$x_q=x_l+x_{aq}$，$x_Q=x_{Ql}+x_{aq}$，消去交轴阻尼绕组电流后，有

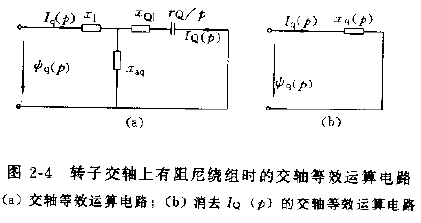
$$\psi_q(p)=x_q(p)I_q(p)$$

其中

$$x_q(p)=x_l+\frac{1}{\frac{1}{x_{aq}}+\frac{1}{x_{Ql}+\frac{r_Q}{p}}}$$

式中$x_q(p)$为交轴运算电抗。交轴等效运算电路如下图所示。

运算电抗特性

同步电抗、瞬变（暂态）电抗和超瞬变（次暂态）电抗

根据上节内容，直轴、交轴运算电抗的等效电路可导出为下图（未消去转子电流）。

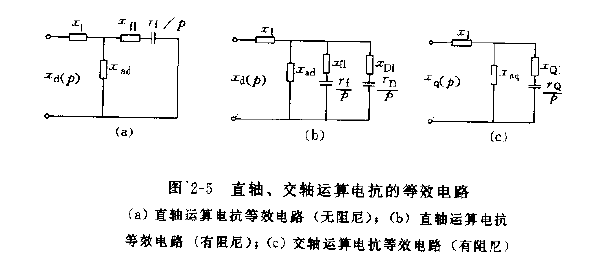
根据拉氏变换终值定理，$p$趋于零时，$t$趋于无穷大，即同步电机稳态运行所呈现的同步电抗。图中$p$趋于零时，其值相当于转子各绕组均断开时的电抗值，即

$$\lim_{p \to 0}x_d(p)=x_l+x_{ad}=x_d$$

$$\lim_{p \to 0}x_q(p)=x_l+x_{aq}=x_q$$

根据拉氏变换初值定理，若转子上无阻尼绕组，根据等效电路，可得

$$\lim_{p \to \infin}x_d(p)=x_l+\frac{1}{\frac{1}{x_{ad}}+\frac{1}{x_{fl}}}=x'_{d}$$

$x'_{d}$即为同步电机的直轴暂态电抗，等效电路如图2-6(a)所示。

若转子上有阻尼绕组，根据等效电路，有

$$\lim_{p \to \infin}x_d(p)=x_l+\frac{1}{\frac{1}{x_{ad}}+\frac{1}{x_{fl}}+\frac{1}{x_{Dl}}}=x''_{d}$$

$x''_{d}$即为同步电机的直轴次暂态电抗，等效电路如图2-6(b)所示。

同理，在交轴方向，根据等效电路，有

$$\lim_{p \to \infin}x_q(p)=x_l+\frac{1}{\frac{1}{x_{aq}}+\frac{1}{x_{Ql}}}=x''_{q}$$

$x''_{q}$即为同步电机的交轴次暂态电抗，等效电路如图2-6©所示。

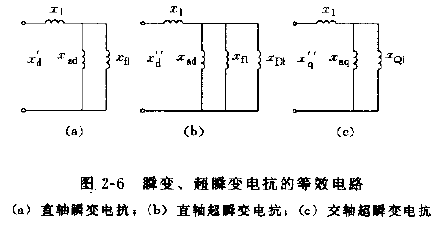
可见，暂态电抗和次暂态电抗分别是无阻尼绕组和有阻尼绕组同步电机在瞬态的初瞬间，从电枢绕组端看进去的电抗。该数值在研究同步电机运行时非常有用。

以时间常数形式来表示的运算电抗

实际应用中，运算电抗$x_d(p)$和$x_q(p)$常用励磁绕组和阻尼绕组的时间常数来表示。

当转子仅有励磁绕组而无阻尼绕组时，有

$$x_d(p)=x_d-\frac{x_{ad}^2p}{r_f+x_fp}=x_d[\frac{r_f+(x_f-x_{ad}^2/x_d)}{r_f+x_fp}]=x_d(\frac{r_f+x_f'p}{r_f+x_fp})=x_d(\frac{1+T_f'p}{1+T_fp})$$

式中，$x_f'$为电枢绕组短路时从励磁绕组端口看进去的瞬态电抗，$T_f'=x_f'/r_f$为励磁绕组瞬态时间常数。$T_f=x_f/r_f$为励磁绕组时间常数。

电枢绕组短路时，从励磁绕组端口看进去的瞬态电抗$x_f'$的等效电路如图2-7所示。

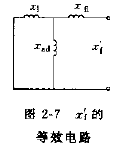
当转子仅有励磁绕组时，其时间常数$T_f'$就是电枢直轴瞬变电流衰减的时间常数$T_d'$，即$T_f'=T_d'$，且$T_f=T_{d0}$。注意：此处时间常数单位均用时间的标幺值表示。

求解瞬变电流时常使用运算电抗的倒数形式，有

$$\frac{1}{x_d(p)}=\frac{1}{x_d} \times \frac{1+T_{d0}}{1+T_d'p}$$

将该式展开为部分分式，并考虑到$x_d'=\frac{T_d'}{T_{d0}}x_d$，有

$$\frac{1}{x_d(p)}=\frac{1}{x_d}+(\frac{1}{x_d'}-\frac{1}{x_d})\frac{T_d'p}{1+T_d'p}$$

该形式在由复数域函数变换返回时域的原函数时非常方便。

同理可推导，转子上除励磁绕组外，直轴上还装有阻尼绕组时的直轴运算电抗$x_d(p)$的时间常数表达式为

$$x_d(p)=x_d[\frac{\sigma_{fD}' T_f' T_D' p^2+(T_f'T_D')p+1}{\sigma_{fD}T_f T_Dp^2+(T_f+T_D)p+1}]$$

式中，

• $T_D$为直轴阻尼绕组本身的时间常数。$T_D=x_D/r_D$
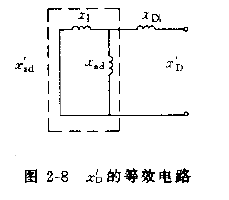
• $T_D'$为励磁绕组开路、直轴电枢绕组短路时，直轴阻尼绕组的时间常数（瞬态时间常数），$T_D'=x_D'/r_D$。
• $T_D'$计算式中$x_D'=x_{Dl}+\frac{1}{\frac{1}{x_l}+\frac{1}{x_{ad}}}=x_{Dl}+x_{ad}'$，为该情况下直轴绕组的等效电抗，$x_D'$等效电路如图2-8所示。

• $\sigma_{fD}$为电枢绕组开路时，励磁绕组和直轴阻尼绕组间的漏磁系数，$\sigma_{fD}=1-{x_{ad}^2}/{x_fx_D}$

• $\sigma_{fD}'$为电枢绕组短路时，励磁绕组和直轴阻尼绕组间的漏磁系数，$\sigma_{fD}'=1-{x_{ad}'^2}/{x_f'x_D'}$

漏磁系数反映绕组间电磁耦合的漏磁情况。当完全耦合无漏磁时，上述漏磁系数为零。实际上每个绕组总存在着只与各自绕组交链的漏磁链和相应的漏电感，因此，漏磁系数不会为零，其大小反映了漏磁的大小。

转子上除励磁绕组外，直轴上还装有阻尼绕组时的直轴运算电抗$x_d(p)$的时间常数表达式可继续分解为$p$的因式形式：

$$x_d(p)=\frac{(T_d'p+1)(T_d''p+1)}{(T_{d0}'p+1)(T_{d0}''p+1)}x_d$$

联立，时间常数由下列$p$的二次方程式确定：

$$(T_{d0}'p+1)(T_{d0}''p+1)=\sigma_{fD}T_fT_Dp^2+(T_f+T_D)p+1$$

$$(T_d'p+1)(T_d''p+1)=\sigma_{fD}'T_f'T_D'p^2+(T_f'+T_D')p+1$$

式中

$$T_{d0}'=\frac{2\sigma_{fD}T_fT_D}{(1-q)(T_f+T_D)}=\frac{1}{2}(1+q)(T_f+T_D)\approx T_f+T_D$$

$$T_{d0}''=\frac{2\sigma_{fD}T_fT_D}{(1+q)(T_f+T_D)} \approx \frac{\sigma_{fD}T_fT_D}{(T_f+T_D)}$$

$$T_d'=\frac{2\sigma_{fD}'T_f'T_D'}{(1-q')(T_f'+T_D')}=\frac{1}{2}(1+q')(T_f'+T_D')\approx T_f'+T_D'$$

$$T_d''=\frac{2\sigma_{fD}'T_f'T_D'}{(1+q')(T_f'+T_D')} \approx \frac{\sigma_{fD}'T_f'T_D'}{(T_f'+T_D')}$$

式中$q\approx1$，$q'\approx1$。

上式中的$T_{d0}'$、$T_{d0}''$、$T_d'$、$T_d''$是同步电机主要的四个时间常数，其准确值计算由上式给出。但以上计算非常繁琐，工程计算角度可进一步简化。考虑阻尼绕组电阻$r_D$标幺值远大于励磁绕组电阻$r_f$的标幺值，而相应的电抗$x_D$、$x_f$的标幺值相近，$x_D'$、$x_f'$的标幺值亦相近，因此在直轴阻尼绕组和励磁绕组的时间常数中，$T_D$远小于$T_f$，且$T_D'$远小于$T_f'$。因而之前的计算式可进一步简化为

$$T_{d0}'=T_f+T_D \approx T_f = T_{d0}$$

$$T_{d0}'' \approx \frac{\sigma_{fD}T_fT_D}{(T_f+T_D)} \approx \sigma_{fD}T_D$$

$$T_d'=T_f'+T_D' \approx T_f'$$

$$T_d'' \approx \frac{\sigma_{fD}'T_f'T_D'}{(T_f'+T_D')} \approx \sigma_{fD}'T_D'$$

进一步可导出

$$T_{d0}'' \approx \sigma_{fD}T_D=(1-\frac{x_{ad}^2}{x_fx_D})\frac{x_D}{r_D}=(x_{Dl}+\frac{1}{\frac{1}{x_{ad}}+\frac{1}{x_{fl}}})\frac{1}{r_D}$$

$$T_d'' \approx \sigma_{fD}'T_D'=(1-\frac{x_{ad}'^2}{x_f'x_D'})\frac{x_D'}{r_D}=(x_D'-\frac{x_{ad}'^2}{x_f'})\frac{1}{r_D}=(x_{Dl}+\frac{1}{\frac{1}{x_{ad}}+\frac{1}{x_l}+\frac{1}{x_{fl}}})\frac{1}{r_D}$$

当直轴设置有阻尼绕组时，从以上对直轴运算电抗$x_d(p)$导出的时间常数的准确计算式可看出，$T_{d0}'$、$T_{d0}''$、$T_d'$、$T_d''$四个时间常数均与励磁绕组和阻尼绕组两个绕组的时间常数有关，因为这两个绕组均放置在转子直轴上，二者之间存在类似于变压器一、二次绕组间的电磁能量传递关系。与变压器不同，同步电机中时间常数$T_D$远小于$T_f$，且$T_D'$远小于$T_f'$，因而可简化，简化后的等效电路见图2-9.

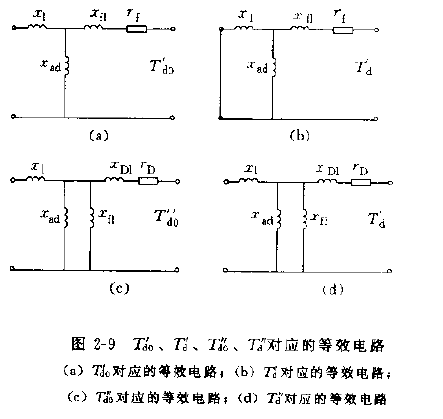
其中，$T_{d0}'$、$T_d'$是电枢绕组分别为开路、短路时励磁绕组的时间常数，二者与阻尼绕组无关；而$T_{d0}''$、$T_d''$是励磁绕组短路，电枢绕组分别为开路、短路时直轴阻尼绕组的时间常数。

为方便逆变换，可导出$x_d(p)$的倒数形式为

$$\frac{1}{x_d(p)}=\frac{1}{x_d}+(\frac{1}{x_d'}-\frac{1}{x_d})\frac{T_d'p}{T_d'p+1}+(\frac{1}{x_d''}-\frac{1}{x_d'})\frac{T_d''p}{T_d''p+1}$$

交轴运算电抗$x_q(p)$的表达式亦可用时间常数表示为

$$x_q(p)=x_q-\frac{x_{aq}^2p}{r_Q+x_Qp}=x_q(\frac{T_q''p+1}{T_{q0}''p+1})$$

式中

• $T_{q0}''$为交轴阻尼绕组本身的时间常数，$T_{q0}''=x_Q/r_Q$
• $T_q''$为考虑到交轴电枢绕组短路时，交轴阻尼绕组的时间常数，$T_q''=\frac{1}{r_Q}(x_{Ql}+x_{aq}x_l/(x_{aq}+x_l))$

$T_{q0}''$和$T_q''$所对应的等效电路如图2-10所示。

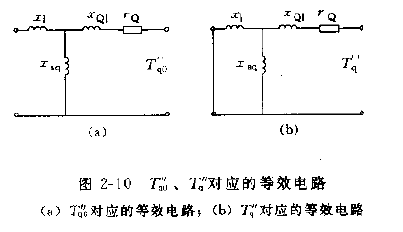
为方便逆变换，可导出$x_q(p)$的倒数形式为

$$\frac{1}{x_q(p)}=\frac{1}{x_q}+(\frac{1}{x_q''}-\frac{1}{x_q})\frac{T_q''p}{1+T_q''p}$$

同步电机的等效电路

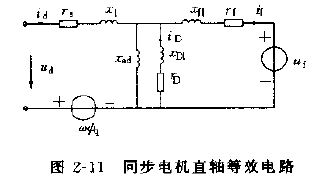
上文已经通过电枢磁链$\psi_d(p)$、$\psi_q(p)$的运算方程式，导出了等效运算电路及相应的运算电抗，在时域中也可画出类似于变压器和感应电机的同步电机等效电路。为获得直轴上各绕组的等效电路，将标幺值表示的直轴磁链方程式代入电压方程式，有

$$\begin{bmatrix} u_d\\u_f\\0 \end{bmatrix}=p \begin{bmatrix} x_d & x_{ad} & x_{ad} \\ x_{ad} & x_f & x_{ad} \\ x_{ad} & x_{ad} & x_D \end{bmatrix} \begin{bmatrix} i_d \\ i_f \\ i_D \end{bmatrix}+ \begin{bmatrix} r_a & 0 & 0 \\ 0 & r_f & 0 \\ 0 & 0 & r_D \\ \end{bmatrix} \begin{bmatrix} i_d \\ i_f \\ i_D \end{bmatrix}+ \begin{bmatrix} -\omega \psi_q \\ 0 \\ 0 \end{bmatrix}$$

相应的直轴等效电路如图2-11所示。

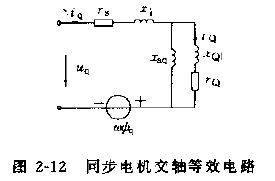
同理可列出交轴电压方程式为

$$\begin{bmatrix} u_q \\ 0 \end{bmatrix}=p \begin{bmatrix} x_q & x_{aq} \\ x_{aq} & x_Q \end{bmatrix} \begin{bmatrix} i_q \\ i_Q \end{bmatrix}+ \begin{bmatrix} r_a & 0 \\ 0 & r_Q \\ \end{bmatrix} \begin{bmatrix} i_q \\ i_Q \end{bmatrix}+ \begin{bmatrix} \omega \psi_d \\ 0 \end{bmatrix}$$

相应的交轴等效电路如图2-12所示。

显然，方程式与等效电路图是对应的，从方程式可画出等效电路，反过来，根据等效电路图，利用基尔霍夫电压定律也可写出各绕组回路的电压方程式。

根据前面分析的结果，分析隐极同步电机时，只要令上面等效电路中$x_{ad}=x_{aq}$，即可使用；分析感应电机时，再将励磁回路取消即可。

下面就图2-11、2-12所示的同步电机等效电路图与通常电机学中感应电机等效电路图的异同比较如下：

• 同步电机等效电路是根据各变量瞬时值写出的电压方程式画出的，可以研究瞬态和稳态问题。通常电机学中感应电机等效电路是根据求解正弦稳态电路的相量方程式画出的，只能求解正弦稳态问题。

• 在频率折算上，稳态感应电机的等效电路是将旋转的转子绕组通过频率折算,把实际转子绕组的频率由$f_2=sf_1$转换为定子绕组频率$f_1$，而同步电机的等效电路是将静止的定子绕组轴线通过坐标变换变为与转子同步旋转的d、q两相绕组轴线，亦即将电枢绕组中频率为$f_1$的交流量转换为频率为零的直流量。

同步电机的功率及电磁转矩

有名值表示三相同步电机电枢端的瞬时输入功率为

$$P=u_ai_a+u_bi_b+u_ci_c$$

标幺值系统中功率基值为

$$P_b=3U_NI_N=\frac{3}{2}U_bI_b$$

因此标幺值表示时电机电枢端瞬时三相输入功率为

$$P^*=\frac{2}{3}(u_a^*i_a^*+u_b^*i_b^*+u_c^*i_c^*)$$

对上式中变量进行Park变换后，dq0坐标系中三相输入功率的标幺值为

$$P^*=u_d^*i_d^*+u_q^*i_q^*+2u_0^*i_0^*$$

dq0坐标系下因定子绕组由原先的“静止绕组”转化为“伪静止绕组”，绕组电感系数由时变系数转为常系数，因而先前在相坐标系统中导出的电磁转矩公式已经不再适用。下面以能量守恒原理为基础重新推导适用于这种绕组的电磁转矩表达式。

由于零轴电流所产生的气隙合成磁场为零，仅产生与电枢绕组交链的漏磁场，因而不参与电磁功率的转换，故在推导电磁转矩时可以不考虑零轴分量。

由dq0坐标系中三相输入功率的标幺值可知，零轴对应的输入功率为$2u_0i_0$，当不考虑电枢零轴分量时，从各端点输入的电功率瞬时值的总和为

$$I'^TU'=u_di_d+u_qi_q+u_fi_f$$

式中

$$I'^T= \begin{bmatrix} i_d & i_q & i_f & i_D & i_Q \end{bmatrix}$$

$$U'= \begin{bmatrix} u_d & u_q & u_f & 0 & 0 \end{bmatrix}^T$$

根据标幺值系统下电压方程式，可导出不考虑电枢零轴分量的电压方程式为

$$U'=L'pI'+\omega G'I'+R'I'$$

式中’上标表示该矩阵未考虑零轴分量，其可以分别从相应的原始矩阵中除去零轴分量的第三行以及第三列得到。如该矩阵方程左乘以电流的转置矩阵$I'^T$，则功率方程为

$$I'^TU'=I'^TL'pI'+I'^T\omega G'I'+I'^TR'I'$$

方程的左边是从各端点输入的总电功率，右边由二项组成：第一项为电流和磁链变化率的乘积，即$I'^TL'pI'=I'^Tp\Psi'$，其代表了定、转子绕组储存磁场能量的变化率；第三项$I'^TR'I'$代表了定、转子绕组的电阻损耗。根据功平衡关系可知，第二项$I'^T\omega G'I'$是跨过气隙由电功率转为机械功率的电磁功率。用转速$\omega$除它，即得到用标么值表示的电磁转矩，即

$$T_{em}=\frac{I'^T\omega G'I'}{\omega}=I'^T G'I'$$

矩阵$G$中第三行和第三列元素均为0，所以有

$$I'^T G'I'=I^TGI$$

即

$$T_{em}=I^TGI$$

该式适用于“伪静止绕组”电机。将电流矩阵$I$和矩阵$G$代入上式，可得三相同步电机的电磁转矩为

$$T_{em}=i_q\psi_d-i_d\psi_q$$