【电机瞬态分析】交流电机在相坐标系统中的状态方程式、电磁转矩和转子运动方程式

交流电机在相坐标系统中的状态方程式

将先前得出的磁链方程式代入电压方程式，即可得到交流电机在相坐标系统中的电压方程式：

$$\begin{bmatrix} u_a \\ u_b \\ u_c \\ u_f \\ u_D \\ u_Q \end{bmatrix}= p \begin{bmatrix} L_{aa} & M_{ab} & M_{ac} & M_{af} & M_{aD} & M_{aQ}\\ M_{ba} & L_{bb} & M_{bc} & M_{bf} & M_{bD} & M_{bQ}\\ M_{ca} & M_{cb} & L_{cc} & M_{cf} & M_{cD} & M_{cQ}\\ M_{fa} & M_{fb} & M_{fc} & L_{f} & M_{fD} & 0 \\ M_{Da} & M_{Db} & M_{Dc} & M_{Df} & L_{D} & 0 \\ M_{Qa} & M_{Qb} & M_{Qc} & 0 & 0 & L_{Q}\\ \end{bmatrix} \begin{bmatrix} i_a\\ i_b\\ i_c\\ i_f\\ i_D\\ i_Q \end{bmatrix}+ \begin{bmatrix} r_a & & & & & \\ & r_b & & & & \\ & & r_c & & & \\ & & & r_f & & \\ & & & & r_D & \\ & & & & & r_Q \\ \end{bmatrix} \begin{bmatrix} i_a\\ i_b\\ i_c\\ i_f\\ i_D\\ i_Q \end{bmatrix}$$

即

$$U=p(LI)+RI$$

矩阵中各绕组的自感系数和互感系数在之前的文章中已有推导。

这是一组表述电机基本电磁关系的时变系数的微分方程组，在已知电感系数和电阻的情况下，利用这组方程就可以求解恒速运转时电机的瞬态和稳态运行问题。由于定子绕组电感系数和定、转子绕组间的互感系数均为位置角$\theta$的函数，即为时间的函数，因此，在求解上述电压方程式时,不能采用解析方法,而需采用数值解法。

用数值法求解微分方程组,可将式$U=p(LI)+RI$改写为状态方程组。状态方程是一组一阶的微分方程式。在电机分析中利用状态变量法时，一般可选取各绕组回路中的电流或磁链作为状态变量，这些变量都是不能突变的量。此处的更多内容请参阅《线性控制理论》。

若选取定子三相电流$i_a$、$i_b$、$i_c$，及转子绕组电流$i_f$、$i_D$、$i_Q$为状态变量，则电压方程式可改写为：

$$U=pLI+RI=(pL)I+LpI+RI$$

式中$pL$为电感系数矩阵的一阶导数。

用状态方程组的标准形式将上式表示如下

$$\dot I = AI + BU$$

式中

$$A=-L^{-1}[D+R]\\ D=pL\\ B=L^{-1}$$

当需要考虑电感系数的高次谐波项时，由于定子绕组的自感系数和互感系数，及定、转子绕组间的互感系数均为位置角$\theta$的无穷三角级数，系数矩阵$L$及其导数$D$的计算工作量很大，用手工计算是不可能的，因而随着计算机技术的发展和广泛应用，可利用计算机求解上述状态方程组的数值解。

相坐标系统下导出的凸极同步电机的电压方程式，只要作相应的变化，就可适用于隐极同步电机和感应电机。隐极同步电机与凸极同步电机的差别是隐极同步电机的气隙为均匀的。感应电机与隐极同步电机相比，定子结构都是相同的，气隙也是均匀的，只是感应电机转子绕组中没有励磁绕组，感应电机的短路转子绕组相当于同步电机的阻尼绕组。所以从凸极同步电机入手推导的方程式，只需作很小的变动，就可以方便地用于隐极同步电机和感应电机。

相坐标系统下交流电机的电压方程式的特点是可以考虑空间气隙磁场谐波，适用于计算磁场谐波很强的电机。利用这些方程，可求解恒速运转时的电机瞬态和稳态运行问题。如果再加上电机的电磁转矩和转子运动方程，电机变速运转时的机电过渡过程也可求解。下节将对电机的电磁转矩和转子运动方程加以讨论。

交流电机电磁转矩和转子运动方程式

电磁转矩是电机进行机电能量转换的关键量，也是表征电机性能的重要量。而转子运动方程是根据牛顿定律写出的作用在电机转子上的转矩之间的平衡方程式，当考虑转子转速变化时，除上述电压方程式外，尚需增加转子运动方程式联立求解。下面先讨论交流电机的电磁转矩。

设交流电机的定子绕组有$m$个回路，以下标"$sm$"表示定子第$m$个回路；转子绕组有$n$个回路，以下标"$rn$"表示定子第$n$个回路。假设磁路为线性，则电机的总磁场能量为

$$W_{m}=\frac{1}{2}(\psi_{s1}i_{s1}+\psi_{s2}i_{s2}+...+\psi_{sm}i_{sm}+\psi_{r1}i_{r1}+\psi_{r2}i_{r2}+...+\psi_{rn}i_{rn})$$

式中各回路的磁链分别为

$$\psi_{s1}=L_{s1}i_{s1}+...+M_{s1sm}i_{sm}+M_{s1r1}i_{r1}+...+M_{s1rn}i_{rn}\\ ...\\ \psi_{sm}=M_{sms1}i_{s1}+...+L_{sm}i_{sm}+M_{smr1}i_{r1}+...+M_{smrn}i_{rn}\\ \psi_{r1}=M_{r1s1}i_{r1}+...+M_{r1sm}i_{sm}+L_{r1}i_{r1}+...+M_{r1rn}i_{rn}\\ ...\\ \psi_{rn}=M_{rns1}i_{s1}+...+M_{rnsm}i_{sm}+M_{rnr1}i_{r1}+...+L_{rn}i_{rn}$$

若改写为矩阵形式，可表示为

$$W_m=\frac{1}{2}I^TLI$$

根据虚位移定理，当各回路电流保持不变时，有

$$f=\frac{\partial W_m}{\partial g}|i=const$$

式中$f$为广义力，$g$为广义位移。

若视广义位移为转子绕组参考轴线领先于定子绕组参考轴线的机械角度$\gamma$，则广义力即为电机的电磁转矩$T_{em}$，有

$$T_{em}=\frac{\partial W_m}{\partial \gamma}=\frac{\partial (\frac{1}{2}I^TLI)}{\partial \gamma}=\frac{1}{2}I^T\frac{\partial L}{\partial \gamma}I$$

电机极对数为$p$，$\theta$为转子绕组参考轴线领先于定子绕组参考轴线的电角度，$\gamma$为同步电机d轴领先于a轴的位置角（机械角度），则有

$$\gamma = \theta / p$$

电磁转矩可继续改写为

$$T_{em}=\frac{p}{2}I^T\frac{\partial L}{\partial \theta}I$$

在建立转子运动方程时，按电动机惯例选用电磁转矩的正方向，它的正方向与转子正常旋转方向一致。如下图；

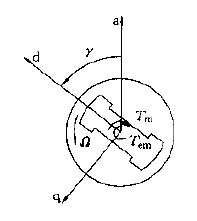
其中$T_{em}$为电动机的电磁转矩，是驱动转矩；$T_m$为负载的机械转矩，是制动转矩；剩余转矩$T_{em}-T_m$则为加速转矩。由此可得转子运动方程为

$$J\frac{d\Omega}{dt}=T_{em}-T_m$$

式中$J$为转动惯量($kgm^2$)，$\Omega$为转子机械角速度，$\Omega=\frac{d\gamma}{dt}$。

电机中常用电弧度来表示角度，将上式改写为：

$$J\frac{1}{p} \times \frac{d\omega}{dt}=J\frac{1}{p} \times \frac{d^2\theta}{dt^2}=T_{em}-T_m$$

式中$\omega$为转子转速($rad/s$)，$\omega = \frac{d\theta}{dt}$。

根据电力拖动内容，若转动部分飞轮转矩为$GD^2$，工程常用单位为$t·m^2$，则

$$J=\frac{1}{4}GD^2 \times 10^3 kgm^2$$

联立转化为状态方程为

$$\frac{d\omega}{dt}=\frac{p}{J}(T_{em}-T_m)\\ \frac{d\theta}{dt}=\omega$$

当需要求解电机变速问题，即$\omega$不为常系数时，需通过联立求解两个状态方程式（上节和本节）得到各状态变量。此时$\theta \neq \omega t + \theta_0$，需通过上式中的第二式解出$\theta$。

转子运动方程式的标幺值形式

工程实践中，转子运动方程式常用标幺值形式。转矩的基值一般选为

$$T_b=\frac{S_N \times 10^3}{\frac{2\pi n}{60}}$$

式中$S_N$为电机额定视在功率($kVA$)，$n$为电机同步转速($r/min$)。

时间基值一般选为$\tau_b=\frac{1}{2\pi f}$，即为电机转过一个电弧度所需的时间。用转矩基值除原式的两侧，可得

$$H\frac{d^2\theta}{dt^2}=H\frac{d\omega^*}{dt^*}=(T_{em}^*-T_m^*)$$

其中$H$被称为惯性常数，可导出为

$$H=\frac{1}{p} \times \frac{GD^2}{S_N}2\pi^3f^2(\frac{n}{60})=2\pi^3f\times \frac{GD^2}{S_N}(\frac{n}{60})^2$$

$H$和时间标幺值之间有简单的关系：

$$dt^*=\frac{Hd\omega^*}{T_{em}^*-T_m^*}$$

假设剩余转矩$T_{em}^*-T_m^*=1$，电机转速从零上升至同步转速($\omega^*=1$)所需的时间为$\tau$，则

$$\tau = \int_{0}^{\tau}dt^*=\int_{0}^{1}Hd\omega^*=H$$

可见，在原来静止的电机转子上加上标幺值为1的剩余转矩后，转速由零上升至同步转速的时间标幺值等于$H$。