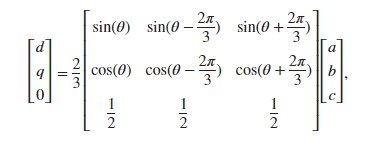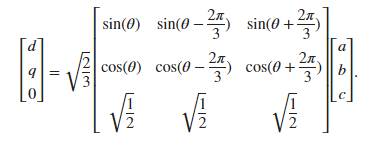【电机瞬态分析】交流电机方程式（dq0坐标系）

概述

上一篇文章对三相凸级同步电机在a、b、c坐标系下的电压方程式和磁链方程式，并且给出了定子和转子绕组之间的电感系数。在需要考虑气隙谐波磁场时，定子绕组的自感系数、互感系数，以及定子绕组和转子绕组之间的互感系数均是关于转子位置角$\theta$的无穷级数。虽然工程中可以忽略高次项进行近似计算，但计算过程仍是非常复杂的。

在仅考虑气隙磁场基波成分的前提下，通过Park变换，用dq0坐标系下的新变量替代原abc相坐标系下的变量，可使定子绕组的自感系数和互感系数又时变系数变为常系数。

交流电机在dq0坐标系中的电压方程式和磁链方程式

相坐标系至dq0坐标系的变换

由线性代数知识，当满秩线性变换时，新变量与原变量间具有单值的对应关系。此时，变换矩阵C（中间量）应为满秩。

满秩矩阵的充分必要条件是其行列式的值不为0。

在此变换下，线性变换和线性反变换式可写为：

$$Y = CX \\ X = C^{-1}Y$$

其中$C^{-1}$是$C$的逆矩阵。

电机工程中最常用的坐标系即为dq0坐标系，即将原来静止的定子绕组a、b、c绕组变换至与转子同角速度旋转的d、q轴线及独立的零轴线代替，如下图所示。

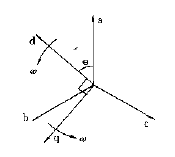
显然在使用dq0坐标系时，由于d、q轴随着转子旋转而与转子轴线呈相对静止，电枢绕组的自感和互感系数变为常数。零轴绕组在电磁方面为独立轴，与其他绕组无耦合关系。

以电枢电流为例，变换后的新变量$i_d$，$i_q$，$i_0$与原变量$i_a$，$i_b$，$i_c$关系为：

$$\left[\begin{array}{l} i_{d} \\ i_{q} \\ i_{0} \end{array}\right]=\frac{2}{3}\left[\begin{array}{ccc} \cos \theta & \cos \left(\theta-\frac{2 \pi}{3}\right) & \cos \left(\theta+\frac{2 \pi}{3}\right) \\ -\sin \theta & -\sin \left(\theta-\frac{2 \pi}{3}\right) & -\sin \left(\theta+\frac{2 \pi}{3}\right) \\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{array}\right]\left[\begin{array}{l} i_{a} \\ i_{b} \\ i_{c} \end{array}\right]$$

式中第三个新变量$i_0$与$i_a$，$i_b$，$i_c$的关系为

$$i_0 = \frac{1}{3}(i_a+i_b+i_c)$$

$i_0$被称为定子绕组电流的零轴分量，为瞬时值。

显然$i_0$与电机各项绕组连接方式有关：

• 有中线连接时，$i_0$实际为电机中线电流的1/3
• 无中线连接时。$i_0$为零

后续分析同步电机及其系统时，若将电流分量变换至dq0坐标系，且原相坐标系中的电压、磁链等量也要同步变换至dq0坐标系，其变换矩阵$C$与电流变量的变换矩阵相同。

磁链方程式（dq0坐标系）

将相坐标系中的磁链方程式转化为dq0坐标系中的磁链方程式，其过程如下：

$$\left[\begin{array}{l} \Psi_{dq0} \\ \Psi_{fDQ} \end{array}\right]=\left[\begin{array}{cc} C & 0 \\ 0 & E \end{array}\right]\left[\begin{array}{l} \Psi_{abc} \\ \Psi_{fDQ} \end{array}\right]=\left[\begin{array}{cc} C & 0 \\ 0 & E \end{array}\right]\left[\begin{array}{cc} L_{ss} & L_{sr} \\ L_{rs} & L_{rr} \end{array}\right]\left[\begin{array}{l} I_{abc} \\ I_{fDQ} \end{array}\right]$$

式中，$\Psi_{dq0}$为电机电枢d、q、0三轴绕组的磁链矩阵表达式，$\Psi_{dq0}=[\phi_d \quad \phi_q \quad \phi_0]^{T}$；$\Psi_{fDQ}$为电机电枢f、D、Q三轴绕组的磁链矩阵表达式，$\Psi_{fDQ}=[\phi_f \quad \phi_D \quad \phi_Q]^{T}$，$E$为单位矩阵。

联立上述各式，可得计算后的结果为：

$$\left[\begin{array}{l} \psi_{d} \\ \psi_{q} \\ \psi_{0} \\ \psi_{f} \\ \psi_{D} \\ \psi_{Q} \end{array}\right]=\left[\begin{array}{cccccc} L_d & 0 & 0 & M_{af0} & M_{aD0} & 0\\ 0 & L_q & 0 & 0 & 0 & M_{aQ0}\\ 0 & 0 & L_0 & 0 & 0 & 0\\ \frac{3}{2}M_{af0} & 0 & 0 & L_f & M_{fD} & 0\\ \frac{3}{2}M_{aD0} & 0 & 0 & M_{Df} & L_{D} & 0\\ 0 & \frac{3}{2}M_{aQ0} & 0 & 0 & 0 & L_Q \end{array}\right]\left[\begin{array}{l} i_{d} \\ i_{q} \\ i_{0} \\ i_{f} \\ i_{D} \\ i_{Q} \end{array}\right]$$

其中

$$L_d = L_{aal}+M_{abl}+\frac{3}{2}L_{mad}=L_{leak} + L_{ad} \\ L_q = L_{aal}+M_{abl}+\frac{3}{2}L_{maq}=L_{leak} + L_{aq} \\ L_0 = L_{aal} - 2M_{abl}$$

式中，$L_{aal}$为电枢a相绕组自漏感系数($l$意为$leak$)，$M_{abl}$为电枢a相和b相绕组之间的互漏感系数，$L_{aad}$为电枢a相绕组自感系数在d轴上的分量，$L_{aaq}$为电枢a相绕组自感系数在q轴上的分量。$M_{af0}$为定子a轴与励磁绕组d轴重合时所具有的最大互感系数，$M_{aD0}$为定子a轴与阻尼绕组D轴重合时所具有的最大互感系数，$M_{aQ0}$为定子a轴与阻尼绕组Q轴重合时所具有的最大互感系数，下标中的“0”表示该互感系数计算时仅考虑了基波分量。

由上式可看出：

• $L_d$和$L_q$分别是假想的电枢d轴绕组和电枢q轴绕组的自感系数。它包括不通过气隙的漏磁链所对应的自漏感系数$L_{leak}=L_{aal}+M_{abl}$以及通过气隙的主磁场所对应的电感系数$L_{ad}=\frac{3}{2}L_{aad}$以及$L_{aq}=\frac{3}{2}L_{aaq}$。

• $L_0$是变换后假想的电枢零轴绕组的自感系数，其仅由漏感系数组成。

• 电枢绕组从abc相绕组轴线转换为与转子同速旋转的d、q轴以及独立的零轴后，电枢绕组的自感系数及互感系数均由时变系数变为与$\theta$角无关的常数。

• 坐标变换使具有相互电磁耦合的abc相绕组变为没有耦合关系的假想的电枢d轴、q轴绕组，达到了解耦的目的。对于电机控制系统，该操作可获得更良好的控制性能。

电压方程式（dq0坐标系）

dq0坐标系中的电压方程式可采用同样的方式从相坐标系统下的电压方程式转换而来，即

$$\left[\begin{array}{l} U_{dq0} \\ U_{fDQ} \end{array}\right]=\left[\begin{array}{cc} C & 0 \\ 0 & E \end{array}\right]\left[\begin{array}{l} U_{abc} \\ U_{fDQ} \end{array}\right]=\left[\begin{array}{cc} C & 0 \\ 0 & E \end{array}\right]\left[\begin{array}{l} p\Psi_{abc} \\ p\Psi_{fDQ} \end{array}\right]+\left[\begin{array}{cc} C & 0 \\ 0 & E \end{array}\right]\left[\begin{array}{cc} R_{abc} & 0 \\ 0 & R_{fDQ} \end{array}\right]\left[\begin{array}{l} I_{abc} \\ I_{fDQ} \end{array}\right]$$

式中，$U_{dq0}$为电枢d、q、0绕组轴端的电压矩阵，$U_{dq0}=[u_d \quad u_q \quad u_0]^{T}$。

上式中等式右侧的第一项：

$$\left[\begin{array}{cc} C & 0 \\ 0 & E \end{array}\right]\left[\begin{array}{l} p\Psi_{abc} \\ p\Psi_{fDQ} \end{array}\right]=\left[\begin{array}{cc} C & (p \quad \Psi_{abc}) \\ p & \Psi_{fDQ} \end{array}\right]$$

根据磁链的Park变换：

$$\Psi_{dq0} = C \Psi_{abc}$$

故有

$$p \Psi_{dq0} = (pC)\Psi_{abc}+C(p \quad \Psi_{abc})$$

可得

$$C(p \quad \Psi_{abc}) = p\Psi_{dq0} - (pC)\Psi_{abc}$$

可以证明其中

$$-(pC)\Psi_{abc} = -{pC}C^{-1}\Psi_{dq0}=\omega \left[\begin{array}{ccc} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 &0 \end{array}\right]\left[\begin{array}{l} \phi_d\\ \phi_q\\ \phi_0 \end{array}\right]=\left[\begin{array}{c} -\omega\psi_q\\ \omega\psi_d\\ 0 \end{array}\right]$$

式中$\omega$为转子的瞬时转速，$\omega = p \theta$。

转换式等式右侧的第二项（即电阻压降）可以写成：

$$\left[\begin{array}{cc} C & 0 \\ 0 & E \end{array}\right]\left[\begin{array}{cc} R_{abc} & 0 \\ 0 & R_{fDQ} \end{array}\right]\left[\begin{array}{c} I_{abc} \\ I_{fDQ} \end{array}\right]= \left[\begin{array}{cc} C & 0 \\ 0 & E \end{array}\right]\left[\begin{array}{cc} R_{abc} & 0 \\ 0 & R_{fDQ} \end{array}\right]\left[\begin{array}{cc} C^{-1} & 0 \\ 0 & E \end{array}\right]\left[\begin{array}{c} I_{dq0} \\ I_{fDQ} \end{array}\right] = \left[\begin{array}{cc} R_{abc} & 0 \\ 0 & R_{fDQ} \end{array}\right]\left[\begin{array}{c} I_{dq0} \\ I_{fDQ} \end{array}\right]$$

联立上述各式，可导出dq0坐标系统下的电压方程式：

$$\begin{bmatrix} u_d \\ u_q \\ u_0 \\ u_f \\ u_D \\ u_Q \end{bmatrix} =p \begin{bmatrix} \psi_d \\ \psi_q \\ \psi_0 \\ \psi_f \\ \psi_D \\ \psi_Q \end{bmatrix} + \begin{bmatrix} r_a & 0 & 0 & 0 & 0 & 0 \\ 0 & r_a & 0 & 0 & 0 & 0 \\ 0 & 0 & r_a & 0 & 0 & 0 \\ 0 & 0 & 0 & r_f & 0 & 0 \\ 0 & 0 & 0 & 0 & r_D & 0 \\ 0 & 0 & 0 & 0 & 0 & r_Q \end{bmatrix} \begin{bmatrix} i_d \\ i_q \\ i_0 \\ i_f \\ i_D \\ i_Q \end{bmatrix} + \begin{bmatrix} -\omega \psi_q \\ \omega \psi_d \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}$$

根据上式，显然假想的电枢d、q轴绕组的电压方程中，与a、b、c绕组的“静止绕组”相比，除$p\psi$仅表示变压器电动势外，另有正比于角速度的运动电动势$\omega\psi$项存在。

在dq0坐标系统中，因重新选取了电枢绕组的轴线，使得d、q轴线以$\omega$转速旋转，而构成d、q绕组的线圈元件仍为静止，因而线圈元件与磁链之间存在相对运动，产生了运动电动势$\omega\psi$。这种绕组轴线与构成该绕组的线圈元件间存在相对运动的绕组称为“伪静止绕组”。

同步电机的派克（Park）方程

派克变换(Park Transform)实际是以克拉克变换(Clark Transform，静止dq坐标系变换)推广而来。恒定幅值条件下的Clark线性变换矩阵即下图所示：

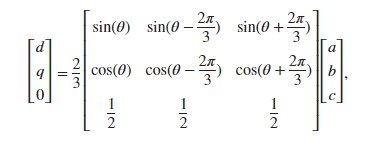
式中，矩阵前的常系数$\frac{2}{3}$用于保证在变换后，变量的幅值仍保持不变。

若需要进行恒功率Clark变换，变换矩阵可被替换为：

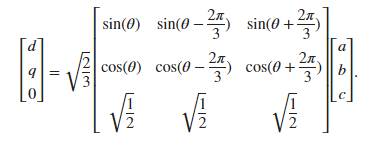
当Clark变换被推广至旋转dq坐标系（即包含转子位置角$\theta$作为变量）时，结合三角恒等变换，可导出Park变换方程。相关推导参见《Clark变换与Park变换的推导》。

Park方程为定常系数微分方程，在同步电机分析中使用该方程可以通过解析方法求解恒速运转时电机的瞬态和稳态运行问题。

上述方程中各变量都是有名值,用有名值的好处是物理念明确,单位的量纲清楚,但在实际计算中往往有所不便,因此，分析计算电机的许多问题时，经常采用标么值。

dq0坐标系统与双反应理论

电机学中已经介绍过，双反应理论是由Andre Blondel提出的一种解释同步电机内部磁场分布的方法。该理论假设同步电机的电枢磁动势（MMF）可以分解为两个独立的分量：

• d轴反应：与转子磁链对齐的磁动势分量，主要影响电机的励磁电流。

• q轴反应：与d轴垂直的磁动势分量，主要影响电机的转矩电流。

双反应理论认为这两个反应是独立的，并且可以分别计算，从而简化了电机的分析。

dq0坐标系统与双反应理论在概念和应用上具有很大的统一性。具体表现如下：

• 坐标对齐：在dq0坐标系统中，d轴和q轴分别对应双反应理论中的d轴反应和q轴反应。这使得电机的磁动势和电流可以通过这两个独立的分量来表示。

• 数学简化：两者都旨在简化电机的数学分析。dq0坐标系统将交流变量转换为直流变量，而双反应理论将复杂的三相系统分解为两个独立的轴。这两种方法结合使用，可以大大简化电机的动态建模和控制设计。

• 独立性假设：双反应理论假设d轴反应和q轴反应是独立的，这在dq0坐标系统中也得到了体现。dq0系统中的电压和电流方程可以分别在d轴和q轴上进行解耦分析。

同步电机的dq0坐标系统和双反应理论都为简化和深入理解电机内部的物理现象提供了工具。dq0坐标系统通过数学变换将电机的时变问题转换为静态问题，而双反应理论则通过物理解释将电机的磁动势分解为两个独立分量。两者在概念和实际应用上具有很强的统一性，结合使用能够更好地分析和控制同步电机。