【电机瞬态分析】交流电机方程式（相坐标）

凸级同步电机在相坐标系统中的电压方程式

正方向规定中的电动机惯例与发电机惯例

电动机惯例

磁链定义式为：

$$\lambda = N \phi$$

其中$N$为线圈匝数。

根据惯例，认为一个线圈轴线的正方向极为该线圈产生磁场轴线的正方向。若按照右手螺旋定律来确定电流和电压的正方向，即认为二者符合电动机惯例，则该回路磁链方程式可列写为：

$$\psi_k = N \phi = L_kI_k$$

其中$L$为线圈电感，$I$为线圈中的电流。

根据电磁感应定理和楞次定理，当磁链$\psi$正向增长时，感生电动势必定是阻止磁链增长的，这也就意味着在等效电路中，电压源电位升高的方向与电流正方向相反。等效回路如下图所示。

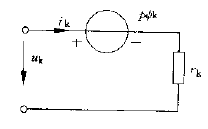
根据基尔霍夫第二定律，此时等效回路的电压方程式为：

$$u_k = p \psi + i_k r_k$$

其中,$p$为微分算子，即$\frac{d}{dt}$。$\psi$为主磁路磁链。

简单来说，电动机惯例下，电压、电流正方向的规定应当反映出：

• 电流从电源流向电机内部。即定子绕组的电流方向是从电源到电机。
• 电源向电机传递功率，电机消耗电能转换为机械能输出。
• 在电动机运行时，电流从定子绕组流入，电枢电流方向与定子磁场方向相同或相近，电动机产生电磁转矩，带动机械负载运行。

发电机惯例

如果保持电流的正方向规定规则不变，仍将产生正向磁链的电流方向规定为电流正方向，仅改变电压正方向的规定，令二者符合发电机惯例，则回路电压正方向与电流正方向的关系改为下图所示：

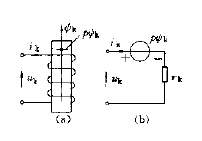
根据基尔霍夫第二定律，回路电压方程式为：

$$u_k = -p \psi - i_k r_k$$

简单来说，发电机惯例下，电压、电流正方向的规定应当反映出：

• 电流从电机内部流向电源。即定子绕组的电流方向是从电机到电网或负载。
• 电机向电源传递功率，电机将机械能转换为电能输出。
• 在发电机运行时，外部机械力驱动转子旋转，定子绕组中的电流流出，定子绕组中的电流方向与定子磁场方向相反或相对，发电机将机械能转换为电能输出到电网或负载。

凸级同步电机的电压方程式

分析凸级同步电机运行问题前，为简化分析，作以下假定：

• 电机铁磁部分的磁路为线性，即不计饱和、剩磁、磁滞和涡流的影响；
• 电机的定、转子齿槽效应用气踪的卡氏系数表征，即认为定、转子表面光滑，只是气隙增大了一些；
• 定子三相绕组对称，转子结构分别对直轴和交轴对称。

由于假定磁路为线性，可应用叠加原理，即某绕组交链的总磁链等于各绕组电流分别产生并与之交链的磁链的代数和。实际电机饱和的影响，可根据电机的运行条件，近似地采用选择适当参数值的方法加以修正。

开始分析前应当规定各变量的正方向，如下图所示。

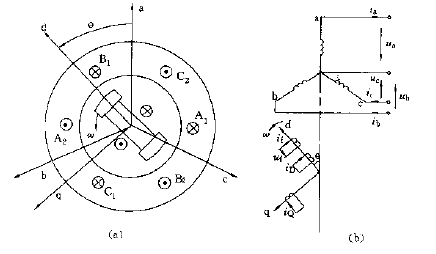
显然图中a、b、c轴线分别表示定子三相绕组实际轴线的对应正方向，即各相绕组磁链正方向。以及为基础，规定产生正向磁链的电流方向为电流正方向。电压正方向与电流正方向的关系按照电动机惯例确定。

定子绕组

按照电动机惯例，根据基尔霍夫第二定律，定子三相绕组的电压方程式可分别根据定子绕组回路列写为：

$$\left.\begin{array}{l} u_{\mathrm{a}}=p \psi_{\mathrm{a}}+r_{s} i_{\mathrm{a}} \\ u_{\mathrm{b}}=p \psi_{\mathrm{b}}+r_{\mathrm{s}} i_{\mathrm{b}} \\ u_{\mathrm{c}}=p \psi_{\mathrm{c}}+r_{\mathrm{s}} i_{\mathrm{c}} \end{array}\right\}$$

励磁绕组

根据电动机惯例，励磁绕组电压方程为：

$$u_f = -p \psi_f - i_f r_f$$

阻尼绕组

阻尼绕组广泛应用于电力系统中需要高稳定性的同步电机，如发电机和大型工业电动机。其主要目的是保证电机在启动、停止以及负载变化时的平稳运行，防止系统失步和振荡。

阻尼绕组一般由安装在磁极极靴上的阻尼条和阻尼环组成，阻尼条由阻尼环部分或全部短接，其分布对于直轴或交轴而言通常都是对称的。其结构、安装位置和简单示意图如下所示。

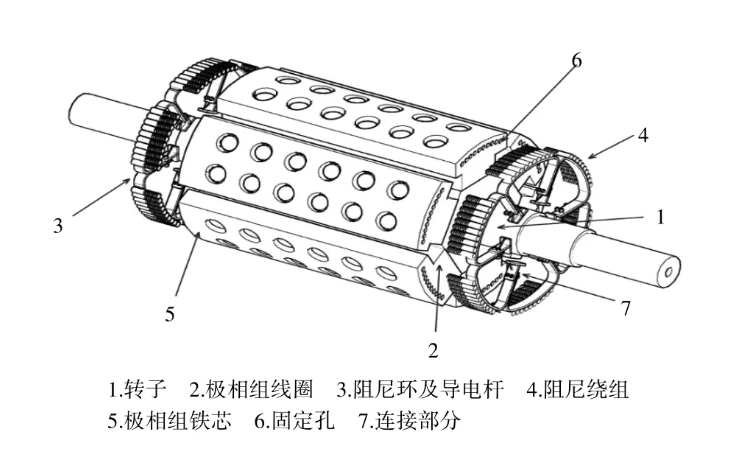
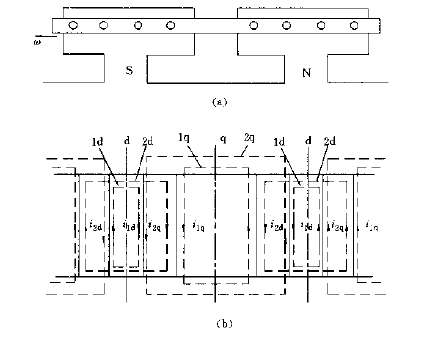
可见阻尼条构成的回路是网状的，为了方便起见，通常电流回路的选取均对称于直轴或交轴。上图表示每个磁极有四根阻尼条的阻尼绕组，其中回路1d、2d对称于d轴，回路1q、2q对称于q轴，阻尼条中流过的实际电流即为相应的d轴和q轴回路电流的代数和。

当只考虑气隙磁场（定、转子合成磁场）基波时，若基于以上规则划分阻尼绕组电流回路，则d轴回路和q轴回路在空间中恰好相差90°的电角度，而转子结构显然相对于d轴或q轴又是对称的，因此在d轴回路和q轴回路之间不产生互感，进而可把实际的阻尼绕组看成是两组假想的阻尼绕组，即直轴阻尼绕组和交轴阻尼绕组。

若按照实际情况单独计算每一根阻尼条的电流和磁链关系，可进一步给出每一根阻尼条的实际电流，但是计算量非常大。在不需研究阻尼绕组内部情况的条件下，可将实际的直轴及轴的多个回路的阻尼绕组分别用一个直轴及交轴的等效阻尼统组D和Q来代替,从而大为简化分析计算工作。这样虽会给计算带来一些误差，但在工程计算中是允许的，也是常用的一种方法。简化的直轴及交轴等效阻尼绕组的电压方程式为：

$$\left.\begin{array}{l} 0 = p \psi_D + r_D i_D \\ 0 = p \psi_Q + r_Q i_Q \end{array}\right\}$$

联立

联立定子绕组、励磁绕组和阻尼绕组的电压方程式，用矩阵形式表示为：

$$U = p \Psi + R I$$

式中

$$U = [u_a \quad u_b \quad u_c \quad u_f \quad 0 \quad 0]^{T}$$

$$I = [i_a \quad i_b \quad i_c \quad i_f \quad i_D \quad i_Q]^{T}$$

$$\Psi = [\psi_a \quad \psi_b \quad \psi_c \quad \psi_f \quad \psi_D \quad \psi_Q]^{T}$$

$$R = \begin{bmatrix} r_a & & & & & \\ & r_b & & & & \\ & & r_c & & & \\ & & & r_f & & \\ & & & & r_D & \\ & & & & & r_Q \\ \end{bmatrix}$$

由上式，每个电压方程式均由两项构成：

• 与绕组交链的主磁链随时间变化而产生的感应电动势$p\psi$
• 电流通过绕组电阻产生的压降$ri$

在上述的分析中，无论是定子绕组、励磁绕组还是阻尼绕组，不管其本身是旋转还是停止，其绕组的轴线与构成该绕组的线圈元件之间永远保持相对静止。这类绕组也被称为“静止绕组” 。

凸级同步电机在相坐标系统中的磁链方程式

上文导出的电压方程式中，与每个绕组交链的主磁链是以下两个部分的代数和：

• 绕组自身通过变化电流产生的磁通（自感）
• 与该绕组相交链的互感磁链（互感）

这些磁链与电流及电感系数的关系用矩阵形式表示为：

$$\begin{bmatrix}\psi_\mathrm{a}\\\psi_\mathrm{b}\\\psi_\mathrm{c}\\\psi_\mathrm{f}\\\psi_\mathrm{D}\\\psi_\mathrm{Q}\end{bmatrix}=\begin{bmatrix}L_\mathrm{aa}&M_\mathrm{ab}&M_\mathrm{ac}&M_\mathrm{af}&M_\mathrm{aD}&M_\mathrm{aQ}\\M_\mathrm{ba}&L_\mathrm{bb}&M_\mathrm{bc}&M_\mathrm{bf}&M_\mathrm{bD}&M_\mathrm{bQ}\\M_\mathrm{ca}&M_\mathrm{cb}&L_\mathrm{cc}&M_d&M_\mathrm{cD}&M_\mathrm{cQ}\\M_\mathrm{fa}&M_\mathrm{fb}&M_\mathrm{fc}&L_\mathrm{f}&M_\mathrm{fD}&0\\M_\mathrm{Da}&M_\mathrm{Db}&M_\mathrm{Dc}&M_\mathrm{Df}&L_\mathrm{D}&0\\M_\mathrm{Qa}&M_\mathrm{Qb}&M_\mathrm{Qc}&0&0&L_\mathrm{Q}\end{bmatrix}\begin{bmatrix}i_\mathrm{a}\\i_\mathrm{b}\\i_\mathrm{c}\\i_\mathrm{f}\\i_\mathrm{D}\\i_\mathrm{Q}\end{bmatrix}$$

注意：矩阵中的公式仍可通过$\lambda = LI$导出，这里的$L$既可以是自感系数也可以是互感系数，其表示意义即为自感磁链或互感磁链。该矩阵中的互感系数也是可逆的。

上式可改写为：

$$\begin{bmatrix}\Psi_{abc}\\\Psi_{fDQ}\end{bmatrix}=\begin{bmatrix}L_{ss}&L_{sr}\\L_{rs} & L_{rr}\end{bmatrix}\begin{bmatrix}I_{abc}\\I_{fDQ}\end{bmatrix}$$

其中，$L_{ss}、L_{sr}$为定、转子自感系数矩阵，$L_{sr}、L_{rs}$为定、转子互感系数矩阵。

显然，由于交轴等效阻尼绕组Q与直轴等效阻尼绕组D，还有励磁绕组$f$的轴线在空间中相差90°电角度，因此二者互感系数为0。这就是为什么矩阵中$M_{fQ}、M_{DQ}、M_{Qf}、M_{QD}$四者均等于0。

凸级同步电机的自感系数与互感系数

磁动势、磁导、自感系数、互感系数

回顾一下磁导的概念：

磁导（magnetic conductance,$\mu$）是衡量磁性材料对磁场线的导通能力的物理量，它类似于电导在电路中的作用。磁导越大，表示材料对磁场线的导通能力越强。具体来说，磁导是磁通量与磁动势的比值，反映了材料在磁场中的导磁性能。磁导越大，说明该部分对磁通量的阻碍越小，即导磁能力越强，磁阻（magnetic reluctance）越小。

磁路中的磁导定义为：$\Lambda = \frac{\Phi}{F}$，其中$\Lambda$为磁导，单位安培每韦伯（$A/Wb$），$\Phi$为磁通量，单位韦伯（$Wb$），$F$为磁动势，单位安培($A$)。

已经自感系数定义为：

$$L = \frac{N\Phi}{I}$$

磁导定义为：

$$\Lambda = \frac{\Phi}{F} = \frac{1}{R_m}$$

根据磁路欧姆定律：

$$F = \Phi R_m = NI$$

式中$F$为作用于该磁路上的磁动势，$\Phi$为磁路内磁通量，$R_m$为磁阻。

联立以上式子，可导出：

$$L = N^2 \Lambda$$

该方法也可被推广至分析两个线圈间互感系数的关系。

由以上推导可知：

• 线圈自感系数为线圈内通过单位电流所产生的自感磁链，其大小与该线圈匝数的平方（$N^2$）及自感磁通所经磁路磁导($\mu$)的乘积成正比
• 线圈1和线圈2间的互感系数为线圈1内通过单位电流所产生的与线圈2相交链的互感磁链，其大小与两线圈匝数的乘积（$N_1N_2$）成正比，并与互感磁通所经磁路的磁导($\mu$)成正比

凸级同步电机在转子旋转时，显然部分绕组之间的相对空间位置以及所对应磁路的磁导随转子位置变化而变化，因此相应的自感系数$L$或互感系数$M$将是转子位置角$\theta$的函数，即时变函数。

定子绕组自感系数

首先分析定子a相绕组的自感系数$L_{aa}$。当绕组匝数确定时，$L_{aa}$的大小主要取决于对应磁路磁导的大小。当a相绕组中轴线与磁极直轴（d轴）轴线重合，即$\theta=0$时，a相绕组磁场对应磁路的磁导$\Lambda$最大，因而在此位置自感系数达到最大值$L_{aad}$；当转子旋转至$\theta = \pi /2$电弧度时，a相绕组轴线与转子q轴重合，对应磁路的磁导最小，自感系数为最小值$L_{aaq}$。当转子旋转至$\theta = \pi$电弧度时，对应磁路的磁导$\Lambda$和自感系数$L$又达到最大值。

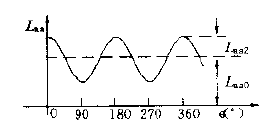
显然a相绕组自感系数随$\theta$的角的变化可以用余弦级数表示为：

$$L_{aa}=L_{aa0}+L_{aa2}cos{2\theta}+L_{aa4}cos{4\theta}+...$$

可见用该种方式计算绕组自感系数非常复杂。就工程设计而言，一般只需考虑气隙的基波磁动势和气隙的基波磁场。

仅考虑隙的基波磁动势和气隙的基波磁场时，a相绕组自感系数$L_{aa}$由以下二者构成：

• 不通过气隙的漏磁场所对应的漏电感$L_{aal}$
• 通过气隙的主合成磁场对应的主电感$L_{aam}$

漏电感$L_{aal}$一般仅和漏磁场的分布情况以及磁路性质有关，与转子空间位置无关，为一常数。主电感$L_{aam}$是关于转子位置角$\theta$的函数。

令a相绕组有效匝数为$W$，由磁动势定义式，绕组线圈通过单位电流所产生的基波磁动势为$F_{am}=W$，轴线为a轴。将该磁动势分解至磁导$\Lambda$为恒值的d轴和q轴上，即$F_{amd}=Wcos\theta$, $F_{amq}=-Wsin\theta$。令d轴和q轴的磁导分别为$\Lambda_d$和$\Lambda_q$，则a相磁动势在d轴和q轴产生的基波磁通大小分别为：

$$\phi_d=F_{amd}\Lambda_d=W\Lambda_d cos\theta\\ \phi_q=F_{amq}\Lambda_q=-W\Lambda_q sin\theta$$

二者与a相绕组交链的自感磁链等于相绕组的有效匝数$W$与d轴、q轴磁通在a轴上的分量乘积的代数和：

$$\Psi_{aam}=W(\phi_d cos\theta-\phi_q sin\theta)=W^2\Lambda_d cos^2{\theta}+W^2\Lambda_q sin^2{\theta}$$

a相绕组通过单位电流时产生的主电感的表达式为：

$$L_{aam}=L_{aad}cos^2{\theta}+L_{aaq}sin^2{\theta}=\frac{1}{2}(L_{aad}+L_{aaq})+\frac{1}{2}(L_{aad}-L_{aaq})cos{2\theta}$$

a相绕组的自感系数$L_{aa}$为主电感$L_{aam}$和漏电感$L_{aal}$的代数和，即

$$L_{aa} = L_{aam} + L_{aal} = L_{aa0}+L_{aa2}cos{2\theta}$$

同理

$$L_{bb} = L_{aa0}+L_{aa2}cos{2(\theta-\frac{2\pi}{3})}\\ L_{cc} = L_{aa0}+L_{aa2}cos{2(\theta+\frac{2\pi}{3})}$$

式中

$$L_{aa0} = L_{aal}+\frac{1}{2}(L_{aad}+L_{aaq})\\ L_{aa2} = \frac{1}{2}(L_{aad}-L_{aaq})$$

显然，当只考虑空间基波磁场时，凸级同步电机三相定子绕组二点自感系数只有常数项和转子位置角$\theta$的二次项，其他高次谐波项不存在，给计算带来很大的方便。

注意：隐级同步电机和感应电机由于具有均匀分布的气隙，故各项绕组的自感系数与转子位置角$\theta$无关，为一常数。

定子两相绕组间的互感系数

定子三相绕组结构相同，但绕组轴线在空间上互差$2\pi/3$电弧度。a相绕组通过单位电流所产生的与b相绕组相交链的互感磁链，此为a、b相的互感系数$M_{ab}$。

互感系数也由两部分构成：

• 与不通过气隙的漏磁通对应的互漏感系数$M_{abl}$
• 与通过气隙的主磁通对应的互感系数$M_{abm}$

与自感系数类似，互漏感系数$M_{abl}$为一常值，互感系数$M_{abm}$随转子位置变化而变化。

上文已经求出仅考虑空间基波磁场分布下a相绕组单位电流产生的直轴磁通$\phi_d$和交轴磁通$\phi_q$。它们与b相绕组相交链的互感磁链，等于相绕组有效匝数$W$与它们在b轴上的磁通量分量乘积的代数和：

$$\begin{aligned} \psi_{\mathrm{abm}} & =W\left[\phi_{d} \cos \left(\theta-\frac{2 \pi}{3}\right)\right]-W\left[\phi_{q} \sin \left(\theta-\frac{2 \pi}{3}\right)\right] \\ & =W^{2} \Lambda_{d} \cos \theta \cos \left(\theta-\frac{2 \pi}{3}\right)+W^{2} \Lambda_{q} \sin \theta \sin \left(\theta-\frac{2 \pi}{3}\right) \end{aligned}$$

所以a相绕组通过单位电路时产生的通过气隙的磁通与b轴绕组相交链的互感磁链，即a、b相间的互感系数为：

$$M_{abm}=L_{aad}cos\theta cos(\theta-\frac{2\pi}{3})+L_{aaq}sin\theta sin(\theta-\frac{2\pi}{3})\\ =-\frac{L_{aad}+L_{aaq}}{4}+\frac{L_{aad}-L_{aaq}}{2}cos(2\theta-\frac{2\pi}{3})$$

a相和b相间的互感系数$M_{ab}$应为互漏电感系数$-M_{abl}$和互电感系数$M_{abm}$之和，即

$$M_{ab}=-M_{abl}-\frac{L_{aad}+L_{aaq}}{4}+\frac{L_{aad}-L_{aaq}}{2}cos(2\theta-\frac{2\pi}{3})\\ = - M_{ab0}+L_{aa2}cos{2(\theta + \frac{2\pi}{3})}$$

同理

$$M_{bc}=- M_{ab0}+L_{aa2}cos{2\theta}\\ M_{ca}=- M_{ab0}+L_{aa2}cos{2(\theta-\frac{2\pi}{3})}$$

式中$M_{ab0} = M_{abl}+\frac{L_{aad}+L_{aaq}}{4}$

由于三相绕组轴线间夹角互为120°电角度，其值大于90°，因此其互感系数均为负值。定子绕组b相和c相间的互感系数$M_{bc}$随转子位置的变化曲线如下图所示。

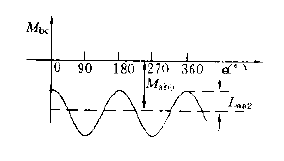
可见，$\theta = 0$时，b相和c相的互感系数的绝对值最小；$\theta = \pi /2$时，互感系数绝对值最大，这与自感系数的变化规律是相反的。

定子绕组和转子绕组间的互感系数

定子绕组和励磁绕组间的互感系数

励磁绕组通过单位电流时所产生的与定子a相绕组交链的互感磁链即为定子绕组与励磁绕组间的互感系数$M_{af}$。互感磁链遵循以下规律：

• 当励磁绕组d轴与a相绕组轴线重合时，互感磁链为最大；
• 转子d轴旋转90°电角度后，两轴线正交，互感磁链为0；
• 当转子d轴旋转180°电角度时，互感磁链为负的最大值；
• 当转子d轴旋转270°电角度时，两轴线正交，互感磁链为0；

因此，一般情况下有：

$$M_{af} = M_{fa} = M_{af0}cos\theta + M_{af3}cos{3\theta}+...$$

同理可推广至b相和c相：

$$M_{bf} = M_{fb} = M_{af0}cos(\theta-\frac{2\pi}{3}) + M_{af3}cos(\theta-\frac{2\pi}{3})+...\\ M_{cf} = M_{fc} = M_{af0}cos(\theta+\frac{2\pi}{3}) + M_{af3}cos(\theta+\frac{2\pi}{3})+...$$

仅考虑基波磁通时，显然互感系数只有基波分量，即：

$$M_{af} = M_{fa} = M_{af0}cos\theta \\ M_{bf} = M_{fb} = M_{af0}cos(\theta-\frac{2\pi}{3})\\ M_{cf} = M_{fc} = M_{af0}cos(\theta+\frac{2\pi}{3})$$

式中$M_{af0}$为a轴与励磁绕组d轴重合时所具有的最大互感系数。下标中的“0”表示该互感系数计算时仅考虑了基波分量。

$M_{af}$随$\theta$的关系如下图所示。

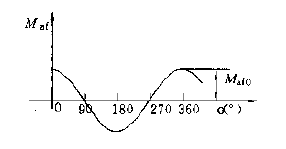
定子绕组与直轴阻尼绕组间的互感系数

直轴阻尼绕组与励磁绕组轴线重合，故定子绕组与直轴阻尼绕组间的互感系数变化规律可由定子绕组与励磁绕组的互感系数变化规律推广得来（仅考虑基波分量）：

$$M_{aD} = M_{Da} = M_{aD0}cos\theta \\ M_{bD} = M_{Db} = M_{aD0}cos(\theta-\frac{2\pi}{3})\\ M_{cD} = M_{Dc} = M_{aD0}cos(\theta+\frac{2\pi}{3})$$

式中$M_{aD0}$为定子绕组a轴与直轴阻尼绕组D轴重合时所具有的最大互感系数。

定子绕组与交轴阻尼绕组间的互感系数

显然交轴提前直轴90°电角度，以$\theta + \frac{\pi}{2}$代换上小节公式中的$\theta$角，并考虑直轴和交轴的磁导不同，推导得（仅考虑基波分量）：

$$M_{aQ} = M_{Qa} = M_{aQ0}cos\theta \\ M_{bQ} = M_{Qb} = M_{aQ0}cos(\theta-\frac{2\pi}{3})\\ M_{cQ} = M_{Qc} = M_{aQ0}cos(\theta+\frac{2\pi}{3})$$

式中$M_{aQ0}$为定子绕组a轴与交轴阻尼绕组Q轴重合时所具有的最大互感系数。

转子绕组的自感系数

转子绕组通过单位电流时产生的自感磁链即为转子绕组的自感系数。由于定子铁心为圆环形，转子上各绕组产生的自感磁链大小与转子位置无关，均为恒值。

励磁绕组自感系数由两部分组成，即

$$L_f = L_{fl} + L_{fm}$$

式中 $L_{fl}$对应励磁绕组漏磁通的漏电感系数，$L_{fm}$对应励磁绕组气隙磁通的主电感系数。

直轴阻尼绕组和交轴阻尼绕组的自感系数分别为：

$$L_D = L_{Dl} + L_{Dm} \\ L_Q = L_{Ql} + L_{Qm}$$

式中 $L_{Dl}$和$L_{Ql}$对应于D、Q绕组漏磁通的漏电感系数，$L_{Dm}$和$L_{Qm}$对应于D、Q绕组气隙磁通的主电感系数。

转子绕组间的互感系数

因转子分别对直轴和交轴对称，且两轴正交，故交轴阻尼绕组Q与直轴阻尼绕组D、励磁绕组$f$间的互感系数为0.绕组D与绕组$f$同在直轴上且式中相对静止，有

$$M_{fD}=M_{Df}=M_{fDl}+M_{fDm}$$

小结

以上讨论的凸极同步电机电感系数，从变化规律上看，可分为三种类型：

• 定子绕组的自感系数和互感系数。其变化周期为$\pi$。引起这类电感系数变化的原因是转子直轴和交轴的磁导不同,当电机转子为圆柱形时,如隐极同步电机及感应电机，转子直轴和交轴的磁导相同，则电感系数$L_{aad}=L_{aaq}$，定子绕组的自感系数和互感系数均为常数，与转子位置角$\theta$无关。

• 定子与转子绕组间的互感系数。其变化周期为2$\pi$。引起这类电感系数变化的原因是定子绕组轴线与转子绕组轴线间有相对运动，导致互感磁链周期性变化。因此，即使在隐极同步电机和感应电机中，这类互感系数仍是转子位置角$\theta$的函数。

• 转子绕组的自感系数与互感系数。由于定子铁心为圆环形，对转子直轴或交轴而言，磁导是不变的，且转子绕组轴线间无相对运动。上述引起电感系数变化的两个原因均不存在，故转子绕组的自感系数与互感系数均为常数。